Combinatorics, Combinatorial Geometry, Cut a Shape / Dissection Problems

Dissection problems involve cutting a given geometric shape into pieces that can be rearranged to form another specified shape, or to satisfy certain conditions (e.g., forming identical pieces). Questions test spatial reasoning and understanding of area preservation.

• Question

  Prove that the given shape cannot be cut into dominoes:

  

  Topics:

  Combinatorics -> Invariants Combinatorics -> Matchings Number Theory -> Division -> Parity (Even/Odd) Proof and Example -> Proof by Contradiction Combinatorics -> Colorings -> Chessboard Coloring Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems

• Question

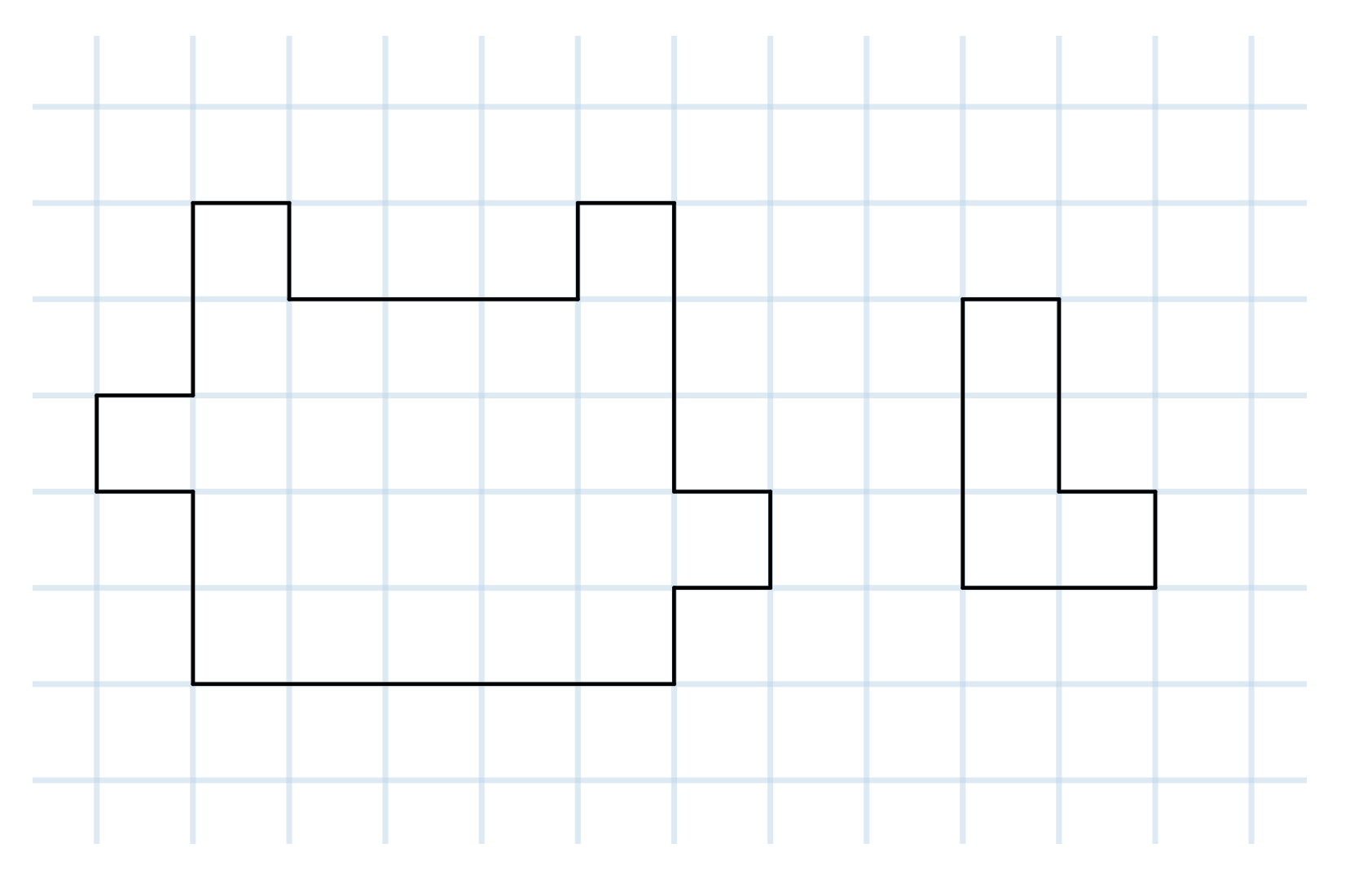
  Can you cut the shape on the left into six shapes like the shape on the right?

  

  Topics:

  Combinatorics -> Invariants Combinatorics -> Matchings Proof and Example Combinatorics -> Colorings -> Chessboard Coloring Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry

• Area of the Shape

  Given a grid paper where the area of each square is one unit area. Find the area of the shape (in unit areas)

   

  

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Plane Geometry Geometry -> Area Calculation Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry
  Sources:
  • Young Mathematician Olympiad, 2017-2018, Stage A, Grades 3-4 Question 7

• Cutting

  What is the largest number of rectangles of size `2 times 5`  that can be cut from a `9 times 9` square?

  Topics:

  Geometry -> Area Calculation Proof and Example -> Constructing an Example / Counterexample Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry
  Sources:
  • Young Mathematician Olympiad, 2018-2019, Stage A, Grades 3-4 Question 1
  • Young Mathematician Olympiad, 2018-2019, Stage A, Grades 5-6 Question 1

• Squares

  You have many cardboard squares of sizes `1 times 1`, `2 times 2`, and `3 times 3`, and you must assemble them into a square of size `7 times 7`.
  What is the smallest possible number of squares you will need?

  Topics:

  Geometry Minimum and Maximum Problems / Optimization Problems Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems
  Sources:
  • Young Mathematician Olympiad, 2018-2019, Stage B, Grades 3-4 Question 5

• Dissect into four parts

  Geometric shapes are called congruent if they coincide when superimposed. Cut the following shape into four congruent parts:

  

  Topics:

  Geometry -> Plane Geometry -> Symmetry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries)
  Sources:
  • Young Mathematician Olympiad, 2019-2020, Final, Grades 3-4 Question 3

• Cut a Boat in Half

  Geometric shapes are called congruent if they coincide when placed on top of each other. Cut the shape into two congruent parts

  

  Topics:

  Geometry -> Plane Geometry -> Symmetry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems
  Sources:
  • Young Mathematician Olympiad, 2019-2020, Final, Grades 5-6 Question 6

• THE SILK PATCHWORK

  The lady members of the Wilkinson family had made a simple patchwork quilt, as a small Christmas present, all composed of square pieces of the same size, as shown in the illustration. It only lacked the four corner pieces to make it complete. Somebody pointed out to them that if you unpicked the Greek cross in the middle and then cut the stitches along the dark joins, the four pieces all of the same size and shape would fit together and form a square. This the reader knows, from the solution in Fig. `39`, is quite easily done. But George Wilkinson suddenly suggested to them this poser. He said, "Instead of picking out the cross entire, and forming the square from four equal pieces, can you cut out a square entire and four equal pieces that will form a perfect Greek cross?" The puzzle is, of course, now quite easy.
  Topics:

  Geometry -> Plane Geometry Geometry -> Area Calculation Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 142

• TWO CROSSES FROM ONE

  Cut a Greek cross into five pieces that will form two such crosses, both of the same size. The solution of this puzzle is very beautiful.
  Topics:

  Geometry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 143

• THE CROSS AND THE TRIANGLE

  Cut a Greek cross into six pieces that will form an equilateral triangle. This is another hard problem, and I will state here that a solution is practically impossible without a previous knowledge of my method of transforming an equilateral triangle into a square (see No. `26`, "Canterbury Puzzles").
  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Triangles Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 144