שלושים ושלוש הפנינים

"אדם שאני מכיר," אמר טדי ניקולסון במסיבת משפחה מסוימת, "ברשותו מחרוזת של שלושים ושלוש פנינים. הפנינה האמצעית היא הגדולה והטובה מכולן, והשאר נבחרו וסודרו כך, שמתחילים מקצה אחד, כל פנינה עוקבת שווה £`100` יותר מקודמתה, ישר עד לפנינה הגדולה. מהקצה השני הפנינים עולות בערכן ב-£`150` עד לפנינה הגדולה. כל המחרוזת שווה £`65,000`. מה ערכה של הפנינה הגדולה הזו?"

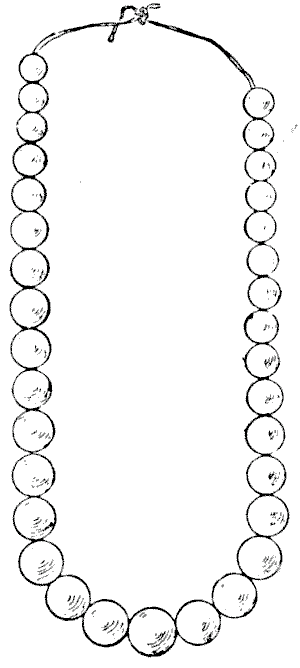
"פנינים ופריטי לבוש אחרים," אמר הדוד וולטר, כשמחיר הפנינה היקרה התגלה, "מזכירים לי את אדם וחווה. הרשויות, ייתכן שאינכם יודעים, חלוקות לגבי מספר התפוחים שנאכלו על ידי אדם וחווה. יש הסבורים שחווה `8` (אכלה) ואדם `2` (גם), סך הכל `10` בלבד. אבל מתמטיקאים מסוימים חישבו זאת אחרת, וטוענים שחווה `8` ואדם סך הכל `16`. עם זאת, החוקרים האחרונים ביותר חושבים שהמספרים הנ"ל שגויים לחלוטין, כי אם חווה `8` ואדם `82`, הסך הכל חייב להיות `90`."

"טוב," אמר הארי, "נראה לי שאם היו ענקים בימים ההם, כנראה חווה `81` ואדם `82`, מה שייתן סך של `163`."

"אני לא מרוצה בכלל," אמרה מוד. "נראה לי שאם חווה `81` ואדם `812`, הם צרכו יחד `893`."

"אני בטוח שכולכם טועים," התעקש מר וילסון, "כי אני חושב שחווה `814` אדם, ואדם `8124` חווה, אז אנחנו מקבלים סך של `8,938`."

"אבל, תראו," התפרץ הרברט. "אם חווה `814` אדם ואדם `81242` מחייב את חווה, בטח הסך הכל היה `82,056`!"

בשלב זה הציע הדוד וולטר שהם יניחו לעניין. הוא הצהיר שזה בבירור מה שמתמטיקאים מכנים בעיה בלתי ניתנת להכרעה.