אלגברה, סדרות, סדרה חשבונית

סדרה חשבונית היא סדרה שבה ההפרש בין איברים עוקבים הוא קבוע (קבוע זה נקרא ההפרש המשותף). שאלות כוללות מציאת האיבר ה-`n`-י, סכום `n` האיברים הראשונים, ההפרש המשותף, או תכונות אחרות על סמך מידע נתון.

• המשיכו את הסדרה

  `2, 6, 12, 20, 30…`

  א. מה המספר הבא (השישי) בסדרה?

  ב. מה המספר ה-`2016` בסדרה?

  נושאים:

  אריתמטיקה לוגיקה -> הגיון אלגברה -> סדרות -> סדרה חשבונית אלגברה -> סדרות -> השלימו\המשיכו סדרה
  מקורות:
  • אתר האינטרנט problems.ru

• שאלה

  בהינתן מספר שלם חיובי N, נתבונן בתהליך הבא: נסמן ב-`S(N)` את סכום הספרות של N ניקח את סכום הספרות של `S(N)`  נחזור על הפעולה שוב ושוב עד שנקבל מספר חד ספרתי נקרא למספר הפעמים שביצענו את התהליך הנ"ל עד שקיבלנו מספר חד-ספרתי: "העומק" של N. לדוגמה, העומק של 49 הוא `S(49)=13 -> S(13)=4)2` , הפעולה בוצעה פעמיים( והעומק של 45 הוא 1.

  א) הוכיחו כי לכל מספר N אכן יש עומק סופי, כלומר, שתמיד יתקבל מספר חד-ספרתי בשלב כלשהו של התהליך.

  ב) נסמן ב-`x(n)` את המספר המינימלי (שערכו הקטן ביותר) בעל עומק N. מצאו את השארית של `x(5776)` בחילוק ב-6 .נמקו את תשובתכם!

  ג) מצאו את השארית של המספר `x(5776) - x(5708)` בחילוק ב-2016 .נמקו את תשובתכם!

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  תורת המספרים -> חשבון השאריות קומבינטוריקה -> אינדוקציה אלגברה -> סדרות -> סדרה חשבונית
  מקורות:
  • אולימפיאדת גיליס, תשע"ו שאלה 3

• שאלה

  מצאו את המסכום של כל המספרים הטבעיים מ-`1` עד `100`.

  נושאים:

  אריתמטיקה אלגברה -> טכניקה אלגברית לוגיקה -> הגיון אלגברה -> סדרות -> סדרה חשבונית

• שאלה

  על הלוח כתובים המספרים: `1, 2, 3, …, 2016, 2017`. תוך מהלך אחד מותר לבחור זוג מספרים שכתובים על הלוח, למחוק אותם ולרשום במקומם את ההפרש שלהם (החיובי). אחרי מספר פעולות כאלו נשאר על הלוח מספר בודד. האם יתכן שזה אפס?

  נושאים:

  אריתמטיקה קומבינטוריקה -> אינווריאנטים קומבינטוריקה -> אינדוקציה תורת המספרים -> חלוקה -> זוגיות אלגברה -> סדרות -> סדרה חשבונית קומבינטוריקה -> בדיקת מקרים -> תהליכים הוכחה ודוגמה -> הוכחה בשלילה

• שאלה

  האם קיימת סדרה חשבונית אינסופית שמורכבת ממספרים ראשוניים בלבד?

  הערה: לא נתיחס לסדרות חשבוניות "טריוויאליות", שהן קבועות.

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  תורת המספרים -> מספרים ראשוניים אלגברה -> סדרות -> סדרה חשבונית הוכחה ודוגמה -> הוכחה בשלילה

• שאלה

  בכמה סכום כל המספרים הזוגיים שלא עוברים את `100` גדול יותר מסכום כל המספרים האי זוגיים שלא עוברים את `100`?

  נושאים:

  אריתמטיקה קומבינטוריקה -> ספירה כפולה אלגברה -> טכניקה אלגברית לוגיקה -> הגיון אלגברה -> סדרות -> סדרה חשבונית

• שאלה

  הוכיחו כי 

  `1+3+5+...+(2n-1)=n^2`

  נושאים:

  קומבינטוריקה -> אינדוקציה אלגברה -> סדרות -> סדרה חשבונית

• מסגרת

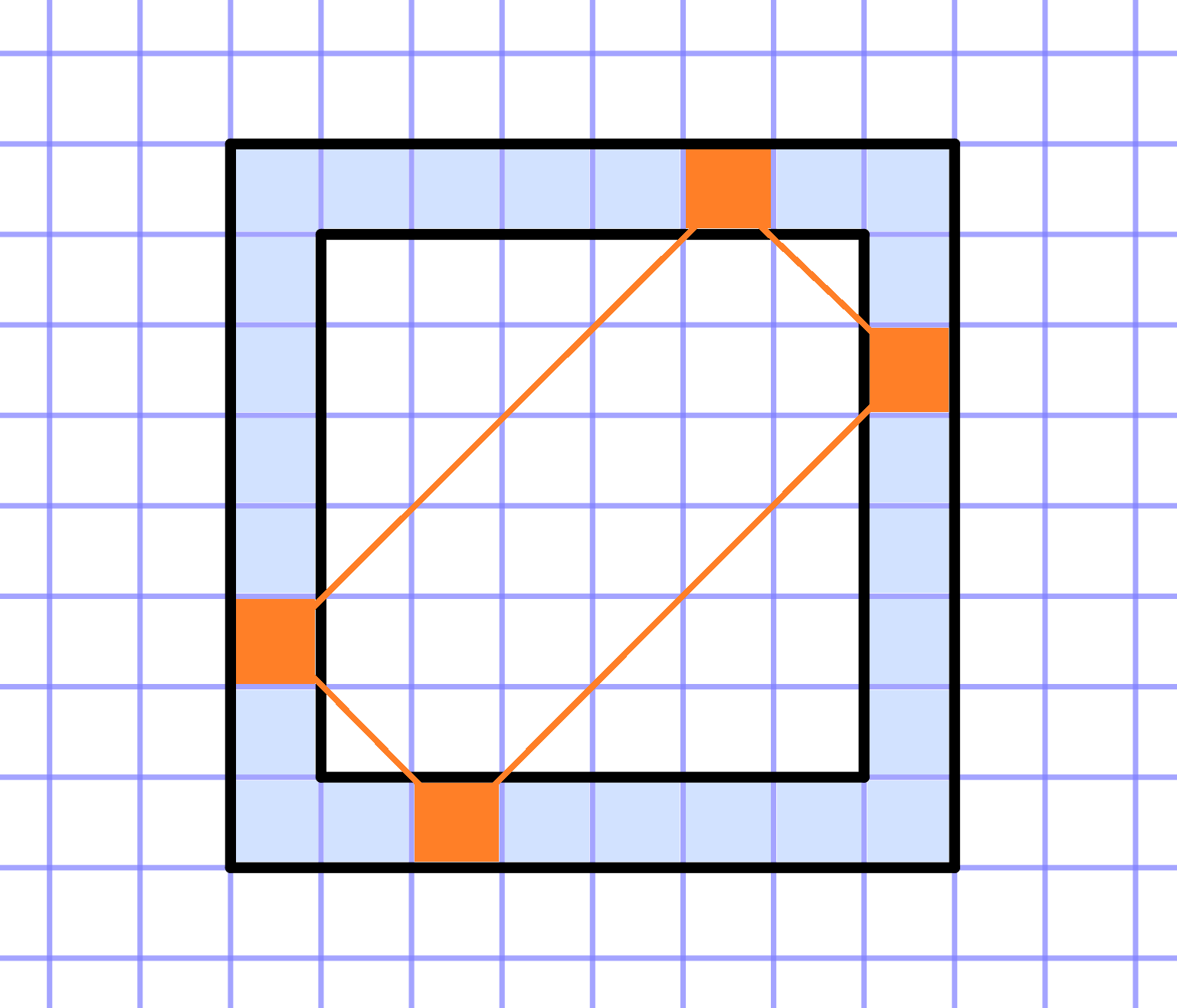
  על דף משבצות נתון ריבוע בגודל `NxxN`. נתבנן במסגרת שלו בעובי של משבצת אחת. היא מורכבת מ-`4*(N-1)` משבצות.

  האם תוכלו לרשום במשבצות של המסגרת `4*(N-1)` מספרים שלמים עוקבים (לא בהכרח חיוביים), כך שיתקיים התנאי הבא:

  לכל מלבן שקודקודיו נמצאים על המסגרת וצלעותיו מקבילים לאלכסונים של הריבוע המקורי, סכום המספרים בקודקודים שווה לגודל קבוע. זה כולל גם את המלבנים "המנוונים" בעלי רוחב אפס שמתלכדים עם האלכסונים של הריבוע - במקרה הזה פשוט סוכמים את שני המספרים בקודקודים המנוגדים של הריבוע

  עבור:

  א. `N=3`

  ב. `N=4`

  ג. `N=5`

  

  נושאים:

  אריתמטיקה תורת המספרים -> חלוקה -> זוגיות הוכחה ודוגמה -> בניית דוגמה אלגברה -> סדרות -> סדרה חשבונית קומבינטוריקה -> בדיקת מקרים -> תהליכים
  מקורות:
  • תחרות הערים, תשמ"ד, סתיו, גרסת תרגול, כיתות ט-י שאלה 3 נקודות 2+3+4

• שאלה

  `120` כדורים זהים מונחים בצורה של פירמידה משולשת. כמה שכבות יש בפירמידה?

  הערה: מדובר בפירמידה, שהיא צורה תלת מימדית, ולא במשולש במישור.

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  גאומטריה -> גאומטריה במרחב אריתמטיקה לוגיקה -> הגיון הוכחה ודוגמה -> בניית דוגמה אלגברה -> סדרות -> סדרה חשבונית אלגברה -> סדרות -> השלימו\המשיכו סדרה תורת המספרים -> מספרים משולשיים

• שאלה

  נתונה הסדרה `1 , 1/2 ,1/3 ,1/4 ,1/5,...`, האם קיימת סדרה חשבונית שמורכבת מאיברי הסדרה הנ"ל

  1. באורך 5

  2. בכל אורך

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  תורת המספרים -> חשבון השאריות -> סימני חלוקה הוכחה ודוגמה -> בניית דוגמה אלגברה -> סדרות -> סדרה חשבונית אריתמטיקה -> שברים תורת המספרים -> המחלק המשותף המקסימלי והכפולה המשותפת המינימלית
  מקורות:
  • תחרות הערים, תשמ"ב, אביב