Number Theory

Number Theory is a branch of mathematics concerned with the properties of integers. Topics include prime numbers, divisibility, congruences (modular arithmetic), Diophantine equations, and functions of integers. Questions often require analytical and creative thinking about numbers.

Prime Numbers Chinese Remainder Theorem Modular Arithmetic / Remainder Arithmetic Greatest Common Divisor (GCD) and Least Common Multiple (LCM) Triangular Numbers Division

• Question

  Three hedgehogs have three pieces of cheese weighing `5`, `8`, and `11` grams. A fox offers to help the hedgehogs divide the cheese equally. The fox can bite off one gram from each of two cheese pieces of its choice. Can the fox, using these actions, reach a state where it leaves the three hedgehogs with equal pieces of cheese?

  Topics:

  Arithmetic Algebra -> Word Problems Proof and Example -> Constructing an Example / Counterexample Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Number Theory -> Division
  Sources:
  • problems.ru web site

• 5 = 6?

  Here is a "proof" that `5` is equal to `6`:

  `35+10-41=42+12-50 `

  `35+10-45=42+12-54 `

  `5*(7+2-9)=6*(7+2-9) `

  ׂ`5=6`

  Where is the mistake?

  Topics:

  Arithmetic Algebra -> Equations Number Theory -> Division

• Question

  How can you divide `7` apples equally among `12` children, if you are not allowed to cut any apple into more than `5` pieces?

  Show hint

  Log in here to receive the hint
  Topics:

  Algebra -> Word Problems Arithmetic -> Fractions Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Number Theory -> Division
  Sources:
  • problems.ru web site

• Clock Tower

  A bell in a clock tower rings `3` times in `12` seconds. How long does it take to ring `6` times?

  Topics:

  Arithmetic Algebra -> Word Problems Logic -> Reasoning / Logic Number Theory -> Division
  Sources:
  • problems.ru web site

• A mistake in the exercise

  Prove that there is an error in the following multiplication problem:

  \(\begin{array}& & & * & * & * & 2 & 7 \\ \times & & & & & * & * \\ \hline & * & * & * & * & * & 6 \\ + & * & * & * & * & * & \\ \hline & * & * & * & * & 4 & 6 \end{array}\)

  Topics:

  Arithmetic Logic -> Reasoning / Logic Proof and Example -> Proof by Contradiction Number Theory -> Division Puzzles and Rebuses -> Reconstruct the Exercise / Cryptarithmetic
  Sources:
  • Beno Arbel Olympiad, 2013, Grade 7 Question 4

• Birds and Seeds

  Nine identical birds eat less than `1001` seeds for lunch, and ten such birds eat more than `1100` seeds for lunch. How many seeds does one bird eat for lunch?

  Topics:

  Algebra -> Inequalities Algebra -> Word Problems Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Number Theory -> Division

• Question

  In Ella's building, there are three entrances and `13` floors (from `0` to `12`, and the apartments are on every floor except the ground floor). In each entrance, on each floor, there are five apartments. Ella lives in apartment number `73`. In which entrance and on which floor does she live?

  Topics:

  Algebra -> Word Problems Number Theory -> Division Arithmetic -> Division with Remainder

• Question

  A cannibal captured `6` people.

  a. In how many different ways can he choose one person for breakfast, one person for lunch, and one person for dinner?

  b. In how many different ways can he choose three people to release them?

  Topics:

  Combinatorics -> Binomial Coefficients and Pascal's Triangle Combinatorics -> Product Rule / Rule of Product Number Theory -> Division

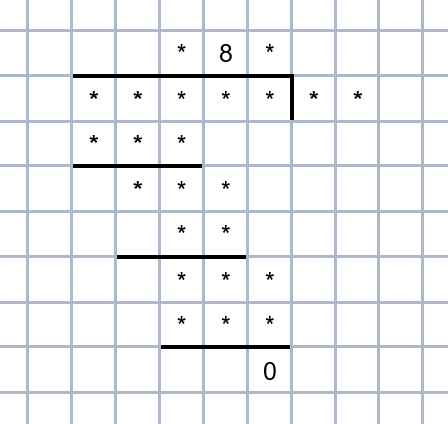
• Reconstruct the Exercise

  Reconstruct the digits in the following exercise:

  

  Topics:

  Arithmetic Number Theory -> Division Puzzles and Rebuses -> Reconstruct the Exercise / Cryptarithmetic

• Long Division

  Calculate the value of the expression and write it as a decimal fraction:

  `1/(1+1/(1+1/(1+1/(1+1/(1))))`

  Topics:

  Arithmetic -> Fractions Number Theory -> Division
  Sources:
  • Young Mathematician Olympiad, 2017-2018, Stage A, Grades 5-6 Question 7