Number Theory

Number Theory is a branch of mathematics concerned with the properties of integers. Topics include prime numbers, divisibility, congruences (modular arithmetic), Diophantine equations, and functions of integers. Questions often require analytical and creative thinking about numbers.

• Question

  Given seven integers `a_1,a_2,a_3,...,a_7`, and let `b_1,b_2,b_3,...,b_7` be the same numbers written in a different order. Prove that the number `(a_1-b_1)(a_2-b_2)*...*(a_7-b_7)` must be even.

  Topics:

  Number Theory -> Division -> Parity (Even/Odd) Proof and Example -> Proof by Contradiction

• Question

  From a chessboard, two opposite corners are removed (the squares `a1` and `h8`, for example). Can you tile the remaining board with dominoes?

  Show hint

  Log in here to receive the hint
  Topics:

  Combinatorics -> Invariants Combinatorics -> Matchings Logic -> Reasoning / Logic Number Theory -> Division -> Parity (Even/Odd) Proof and Example -> Proof by Contradiction Combinatorics -> Colorings -> Chessboard Coloring Puzzles and Rebuses

• Question

  Prove that the product of two consecutive numbers is always even.

  Topics:

  Number Theory -> Division -> Parity (Even/Odd) Proof and Example

• Question

  The following numbers are written on the board: `1, 2, 3, …, 2016, 2017`. In one move, it is allowed to choose a pair of numbers written on the board, erase them, and write their (positive) difference in their place. After several such operations, a single number remains on the board. Is it possible that this is zero?

  Topics:

  Arithmetic Combinatorics -> Invariants Combinatorics -> Induction (Mathematical Induction) Number Theory -> Division -> Parity (Even/Odd) Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Proof and Example -> Proof by Contradiction

• Frame

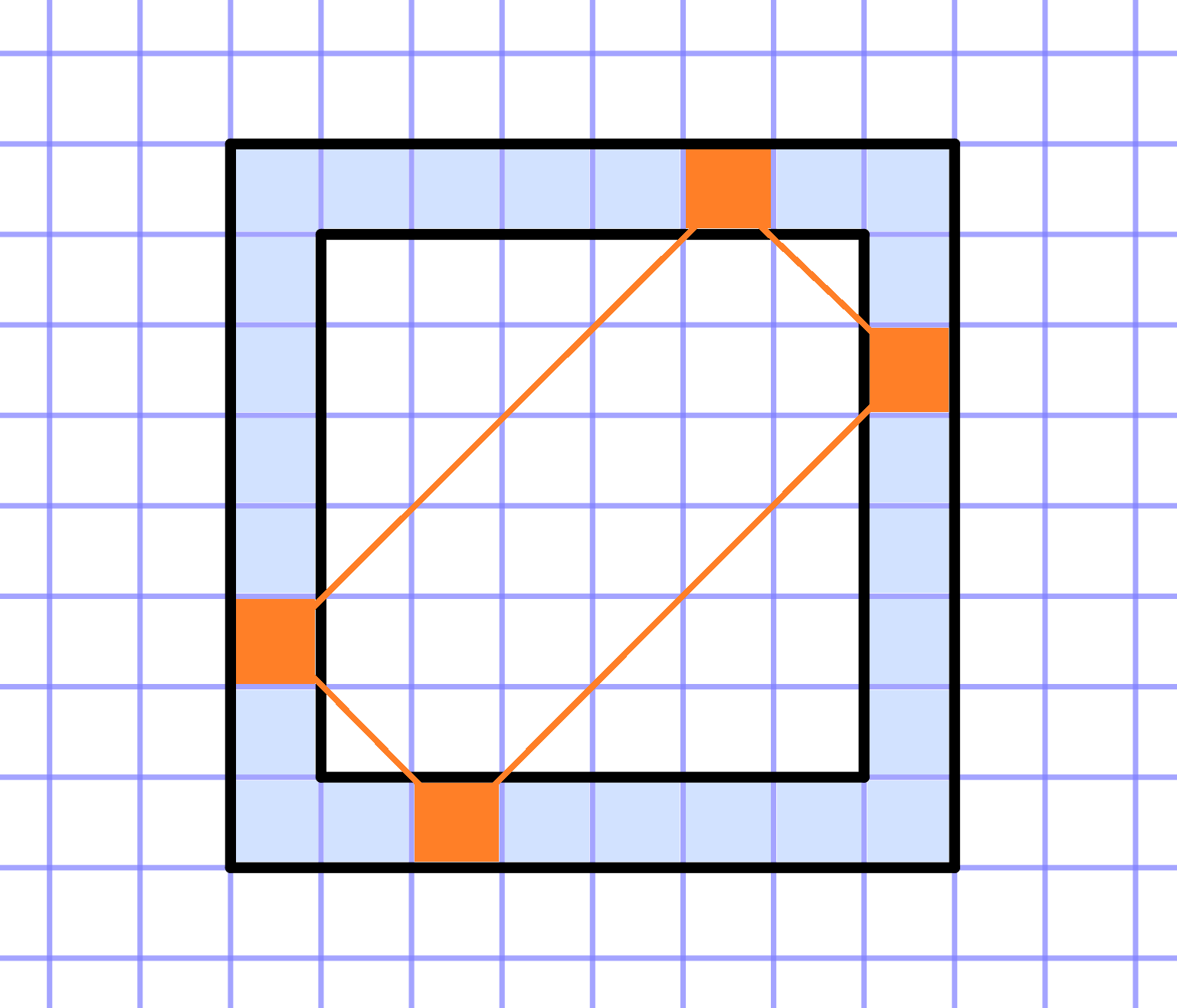
  On a grid paper, a square of size `NxxN` is given. Consider its frame with a width of one square. It consists of `4*(N-1)` squares.

  Can you write `4*(N-1)` consecutive integers (not necessarily positive) in the squares of the frame, such that the following condition holds:

  For every rectangle whose vertices are on the frame and whose sides are parallel to the diagonals of the original square, the sum of the numbers at the vertices is equal to a constant value. This also includes the "degenerate" rectangles of zero width that coincide with the diagonals of the square - in this case, simply sum the two numbers at the opposite vertices of the square.

  For:

  a. `N=3`

  b. `N=4`

  c. `N=5`

  

  Topics:

  Arithmetic Number Theory -> Division -> Parity (Even/Odd) Proof and Example -> Constructing an Example / Counterexample Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures
  Sources:
  • Tournament of Towns, 1983-1984, Fall, Practice Version, Grades 9-10 Question 3 Points 2+3+4

• Question

  Prove that the given shape cannot be cut into dominoes:

  

  Topics:

  Combinatorics -> Invariants Combinatorics -> Matchings Number Theory -> Division -> Parity (Even/Odd) Proof and Example -> Proof by Contradiction Combinatorics -> Colorings -> Chessboard Coloring Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems

• Question

  Each of seven children holds two balloons, one red and one yellow. Can they exchange balloons so that each child has two balloons of the same color?

  Topics:

  Logic -> Reasoning / Logic Number Theory -> Division -> Parity (Even/Odd)

• Question

  `19` apple trees are arranged in a circle. Prove that there exists a pair of adjacent trees such that the total number of apples on them is even.

  Topics:

  Logic -> Reasoning / Logic Number Theory -> Division -> Parity (Even/Odd) Proof and Example -> Proof by Contradiction

• Question

  In the magical land, there are only coins of `4`, `7`, and `10` liras. Shlomi currently only has coins of `4` and `10` liras. Shlomi wants to buy a book that costs `23` liras. Will he be able to pay for the book without change?

  Topics:

  Logic -> Reasoning / Logic Number Theory -> Division -> Parity (Even/Odd)

• Question

  Can you find two numbers such that both their sum and their product are odd? Justify your answer or provide an example!

  Topics:

  Number Theory -> Division -> Parity (Even/Odd) Proof and Example -> Proof by Contradiction