Arithmetic

Arithmetic is the fundamental branch of mathematics dealing with numbers and the basic operations: addition, subtraction, multiplication, and division. Questions involve performing these operations, understanding number properties (like integers, fractions, decimals), and solving related word problems.

Fractions Percentages Division with Remainder

  • DIGITAL DIVISION

    It is another good puzzle so to arrange the nine digits (the nought excluded) into two groups so that one group when divided by the other produces a given number without remainder. For example, `1` `3` `4` `5` `8` divided by `6` `7` `2` `9` gives `2`. Can the reader find similar arrangements producing `3, 4, 5, 6, 7, 8`, and `9` respectively? Also, can he find the pairs of smallest possible numbers in each case? Thus, `1` `4` `6` `5` `8` divided by `7` `3` `2` `9` is just as correct for `2` as the other example we have given, but the numbers are higher. Sources:

  • ADDING THE DIGITS

    If I write the sum of money, £`987, 5`s. `4`½d.., and add up the digits, they sum to `36`. No digit has thus been used a second time in the amount or addition. This is the largest amount possible under the conditions. Now find the smallest possible amount, pounds, shillings, pence, and farthings being all represented. You need not use more of the nine digits than you choose, but no digit may be repeated throughout. The nought is not allowed. Sources:

  • DIGITAL SQUARE NUMBERS

    Here are the nine digits so arranged that they form four square numbers: `9, 81, 324, 576`. Now, can you put them all together so as to form a single square number—(I) the smallest possible, and (II) the largest possible? Sources:

  • THE MYSTIC ELEVEN

    Can you find the largest possible number containing any nine of the ten digits (calling nought a digit) that can be divided by `11` without a remainder? Can you also find the smallest possible number produced in the same way that is divisible by `11`? Here is an example, where the digit `5` has been omitted: `896743012`. This number contains nine of the digits and is divisible by `11`, but it is neither the largest nor the smallest number that will work.

    Sources:

  • THE DIGITAL CENTURY

    `1\ 2\ 3\ 4\ 5\ 6\ 7\ 8\ 9 = 100`.

    It is required to place arithmetical signs between the nine figures so that they shall equal `100`. Of course, you must not alter the present numerical arrangement of the figures. Can you give a correct solution that employs (`1`) the fewest possible signs, and (`2`) the fewest possible separate strokes or dots of the pen? That is, it is necessary to use as few signs as possible, and those signs should be of the simplest form. The signs of addition and multiplication (+ and ×) will thus count as two strokes, the sign of subtraction (-) as one stroke, the sign of division (÷) as three, and so on.

    Sources:

  • THE DICE NUMBERS

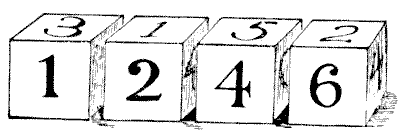
    I have a set of four dice, not marked with spots in the ordinary way, but with Arabic figures, as shown in the illustration. Each die, of course, bears the numbers `1` to `6`. When put together they will form a good many, different numbers. As represented they make the number `1246`. Now, if I make all the different four-figure numbers that are possible with these dice (never putting the same figure more than once in any number), what will they all add up to? You are allowed to turn the `6` upside down, so as to represent a `9`. I do not ask, or expect, the reader to go to all the labour of writing out the full list of numbers and then adding them up. Life is not long enough for such wasted energy. Can you get at the answer in any other way?

    Sources:

  • THE THIRTY-THREE PEARLS

    "A man I know," said Teddy Nicholson at a certain family party, "possesses a string of thirty-three pearls. The middle pearl is the largest and best of all, and the others are so selected and arranged that, starting from one end, each successive pearl is worth £`100` more than the preceding one, right up to the big pearl. From the other end the pearls increase in value by £`150` up to the large pearl. The whole string is worth £`65,000`. What is the value of that large pearl?"

     

    "Pearls and other articles of clothing," said Uncle Walter, when the price of the precious gem had been discovered, "remind me of Adam and Eve. Authorities, you may not know, differ as to the number of apples that were eaten by Adam and Eve. It is the opinion of some that Eve `8` (ate) and Adam `2` (too), a total of `10` only. But certain mathematicians have figured it out differently, and hold that Eve `8` and Adam a total of `16`. Yet the most recent investigators think the above figures entirely wrong, for if Eve `8` and Adam `82`, the total must be `90`."

    "Well," said Harry, "it seems to me that if there were giants in those days, probably Eve `81` and Adam `82`, which would give a total of `163`."

    "I am not at all satisfied," said Maud. "It seems to me that if Eve `81` and Adam `812`, they together consumed `893`."

    "I am sure you are all wrong," insisted Mr. Wilson, "for I consider that Eve `814` Adam, and Adam `8124` Eve, so we get a total of `8,938`."

    "But, look here," broke in Herbert. "If Eve `814` Adam and Adam `81242` oblige Eve, surely the total must have been `82,056`!"

    At this point Uncle Walter suggested that they might let the matter rest. He declared it to be clearly what mathematicians call an indeterminate problem.

    Sources:

  • CATCHING THE THIEF

    "Now, constable," said the defendant's counsel in cross-examination," you say that the prisoner was exactly twenty-seven steps ahead of you when you started to run after him?"

    "Yes, sir."

    "And you swear that he takes eight steps to your five?"

    "That is so."

    "Then I ask you, constable, as an intelligent man, to explain how you ever caught him, if that is the case?"

    "Well, you see, I have got a longer stride. In fact, two of my steps are equal in length to five of the prisoner's. If you work it out, you will find that the number of steps I required would bring me exactly to the spot where I captured him."

    Here the foreman of the jury asked for a few minutes to figure out the number of steps the constable must have taken. Can you also say how many steps the officer needed to catch the thief?

    Sources:

  • THE MUDDLETOWN ELECTION

    At the last Parliamentary election at Muddletown `5,473` votes were polled. The Liberal was elected by a majority of `18` over the Conservative, by `146` over the Independent, and by `575` over the Socialist. Can you give a simple rule for figuring out how many votes were polled for each candidate? Sources:

  • THE ABBOT'S PUZZLE

    The first English puzzlist whose name has come down to us was a Yorkshireman—no other than Alcuin, Abbot of Canterbury (A.D. `735-804`). Here is a little puzzle from his works, which is at least interesting on account of its antiquity. "If `100` bushels of corn were distributed among `100` people in such a manner that each man received three bushels, each woman two, and each child half a bushel, how many men, women, and children were there?"

    Now, there are six different correct answers, if we exclude a case where there would be no women. But let us say that there were just five times as many women as men, then what is the correct solution?

    Sources: