Arithmetic

Arithmetic is the fundamental branch of mathematics dealing with numbers and the basic operations: addition, subtraction, multiplication, and division. Questions involve performing these operations, understanding number properties (like integers, fractions, decimals), and solving related word problems.

Fractions Percentages Division with Remainder

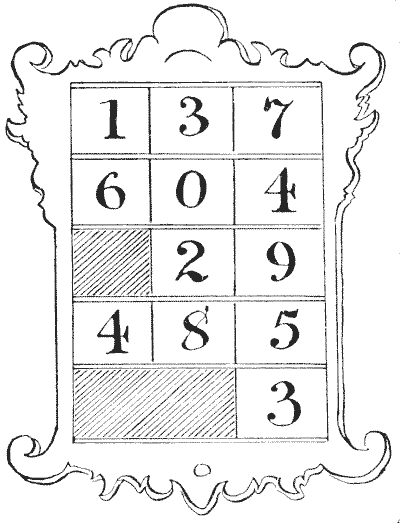
  • THE MANDARIN'S "T" PUZZLE

     

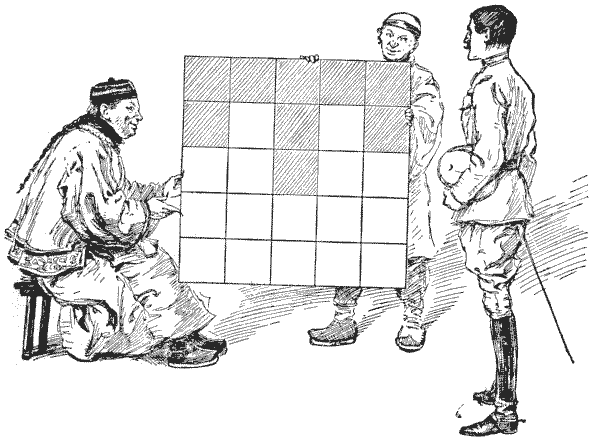
    Before Mr. Beauchamp Cholmondely Marjoribanks set out on his tour in the Far East, he prided himself on his knowledge of magic squares, a subject that he had made his special hobby; but he soon discovered that he had never really touched more than the fringe of the subject, and that the wily Chinee could beat him easily. I present a little problem that one learned mandarin propounded to our traveller, as depicted on the last page.

    The Chinaman, after remarking that the construction of the ordinary magic square of twenty-five cells is "too velly muchee easy," asked our countryman so to place the numbers `1` to `25` in the square that every column, every row, and each of the two diagonals should add up `65`, with only prime numbers on the shaded "T." Of course the prime numbers available are `1, 2, 3, 5, 7, 11, 13, 17, 19`, and `23`, so you are at liberty to select any nine of these that will serve your purpose. Can you construct this curious little magic square?

    Sources:

  • THE TIRING IRONS

     

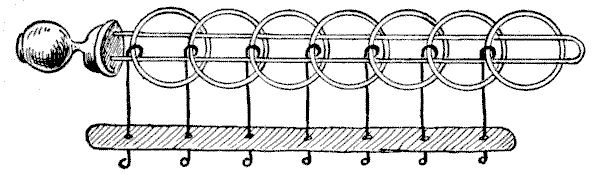
    The illustration represents one of the most ancient of all mechanical puzzles. Its origin is unknown. Cardan, the mathematician, wrote about it in `1550`, and Wallis in `1693`; while it is said still to be found in obscure English villages (sometimes deposited in strange places, such as a church belfry), made of iron, and appropriately called "tiring-irons," and to be used by the Norwegians to-day as a lock for boxes and bags. In the toyshops it is sometimes called the "Chinese rings," though there seems to be no authority for the description, and it more frequently goes by the unsatisfactory name of "the puzzling rings." The French call it "Baguenaudier."

    The puzzle will be seen to consist of a simple loop of wire fixed in a handle to be held in the left hand, and a certain number of rings secured by wires which pass through holes in the bar and are kept there by their blunted ends. The wires work freely in the bar, but cannot come apart from it, nor can the wires be removed from the rings. The general puzzle is to detach the loop completely from all the rings, and then to put them all on again.

    Now, it will be seen at a glance that the first ring (to the right) can be taken off at any time by sliding it over the end and dropping it through the loop; or it may be put on by reversing the operation. With this exception, the only ring that can ever be removed is the one that happens to be a contiguous second on the loop at the right-hand end. Thus, with all the rings on, the second can be dropped at once; with the first ring down, you cannot drop the second, but may remove the third; with the first three rings down, you cannot drop the fourth, but may remove the fifth; and so on. It will be found that the first and second rings can be dropped together or put on together; but to prevent confusion we will throughout disallow this exceptional double move, and say that only one ring may be put on or removed at a time.

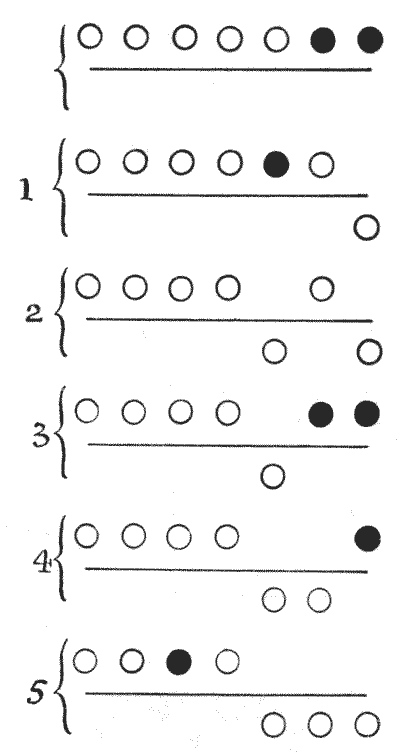
    We can thus take off one ring in `1` move; two rings in `2` moves; three rings in `5` moves; four rings in `10` moves; five rings in `21` moves; and if we keep on doubling (and adding one where the number of rings is odd) we may easily ascertain the number of moves for completely removing any number of rings. To get off all the seven rings requires `85` moves. Let us look at the five moves made in removing the first three rings, the circles above the line standing for rings on the loop and those under for rings off the loop.

    Drop the first ring; drop the third; put up the first; drop the second; and drop the first—`5` moves, as shown clearly in the diagrams. The dark circles show at each stage, from the starting position to the finish, which rings it is possible to drop. After move `2` it will be noticed that no ring can be dropped until one has been put on, because the first and second rings from the right now on the loop are not together. After the fifth move, if we wish to remove all seven rings we must now drop the fifth. But before we can then remove the fourth it is necessary to put on the first three and remove the first two. We shall then have `7, 6, 4, 3` on the loop, and may therefore drop the fourth. When we have put on `2` and `1` and removed `3, 2, 1`, we may drop the seventh ring. The next operation then will be to get `6, 5, 4, 3, 2, 1` on the loop and remove `4, 3, 2, 1`, when `6` will come off; then get `5, 4, 3, 2, 1` on the loop, and remove `3, 2, 1`, when `5` will come off; then get `4, 3, 2, 1` on the loop and remove `2, 1`, when `4` will come off; then get `3, 2, 1` on the loop and remove `1`, when `3` will come off; then get `2, 1` on the loop, when `2` will come off; and `1` will fall through on the 85th move, leaving the loop quite free. The reader should now be able to understand the puzzle, whether or not he has it in his hand in a practical form.

     

    The particular problem I propose is simply this. Suppose there are altogether fourteen rings on the tiring-irons, and we proceed to take them all off in the correct way so as not to waste any moves. What will be the position of the rings after the `9`,999th move has been made?

    Sources:

  • SUCH A GETTING UPSTAIRS

    In a suburban villa there is a small staircase with eight steps, not counting the landing. The little puzzle with which Tommy Smart perplexed his family is this. You are required to start from the bottom and land twice on the floor above (stopping there at the finish), having returned once to the ground floor. But you must be careful to use every tread the same number of times. In how few steps can you make the ascent? It seems a very simple matter, but it is more than likely that at your first attempt you will make a great many more steps than are necessary. Of course you must not go more than one riser at a time.

    Tommy knows the trick, and has shown it to his father, who professes to have a contempt for such things; but when the children are in bed the pater will often take friends out into the hall and enjoy a good laugh at their bewilderment. And yet it is all so very simple when you know how it is done.

    Sources:

  • A CHAIN PUZZLE

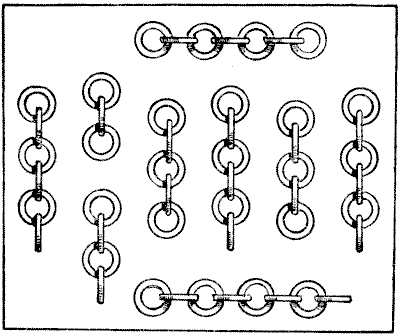    This is a puzzle based on a pretty little idea first dealt with by the late Mr. Sam Loyd. A man had nine pieces of chain, as shown in the illustration. He wanted to join these fifty links into one endless chain. It will cost a penny to open any link and twopence to weld a link together again, but he could buy a new endless chain of the same character and quality for `2`s. `2`d. What was the cheapest course for him to adopt? Unless the reader is cunning he may find himself a good way out in his answer. Sources:

  • THE HYMN-BOARD POSER

    The worthy vicar of Chumpley St. Winifred is in great distress. A little church difficulty has arisen that all the combined intelligence of the parish seems unable to surmount. What this difficulty is I will state hereafter, but it may add to the interest of the problem if I first give a short account of the curious position that has been brought about. It all has to do with the church hymn-boards, the plates of which have become so damaged that they have ceased to fulfil the purpose for which they were devised. A generous parishioner has promised to pay for a new set of plates at a certain rate of cost; but strange as it may seem, no agreement can be come to as to what that cost should be. The proposed maker of the plates has named a price which the donor declares to be absurd. The good vicar thinks they are both wrong, so he asks the schoolmaster to work out the little sum. But this individual declares that he can find no rule bearing on the subject in any of his arithmetic books. An application having been made to the local medical practitioner, as a man of more than average intellect at Chumpley, he has assured the vicar that his practice is so heavy that he has not had time even to look at it, though his assistant whispers that the doctor has been sitting up unusually late for several nights past. Widow Wilson has a smart son, who is reputed to have once won a prize for puzzle-solving. He asserts that as he cannot find any solution to the problem it must have something to do with the squaring of the circle, the duplication of the cube, or the trisection of an angle; at any rate, he has never before seen a puzzle on the principle, and he gives it up.

     

    This was the state of affairs when the assistant curate (who, I should say, had frankly confessed from the first that a profound study of theology had knocked out of his head all the knowledge of mathematics he ever possessed) kindly sent me the puzzle.

    A church has three hymn-boards, each to indicate the numbers of five different hymns to be sung at a service. All the boards are in use at the same service. The hymn-book contains `700` hymns. A new set of numbers is required, and a kind parishioner offers to present a set painted on metal plates, but stipulates that only the smallest number of plates necessary shall be purchased. The cost of each plate is to be `6`d., and for the painting of each plate the charges are to be: For one plate, `1`s.; for two plates alike, `11`¾d. each; for three plates alike, `11`½d. each, and so on, the charge being one farthing less per plate for each similarly painted plate. Now, what should be the lowest cost?

    Readers will note that they are required to use every legitimate and practical method of economy. The illustration will make clear the nature of the three hymn-boards and plates. The five hymns are here indicated by means of twelve plates. These plates slide in separately at the back, and in the illustration there is room, of course, for three more plates.

    Sources:

  • THE GARDENER AND THE COOK

    A correspondent, signing himself "Simple Simon," suggested that I should give a special catch puzzle in the issue of The Weekly Dispatch for All Fools' Day, `1900`. So I gave the following, and it caused considerable amusement; for out of a very large body of competitors, many quite expert, not a single person solved it, though it ran for nearly a month.

     

    "The illustration is a fancy sketch of my correspondent, 'Simple Simon,' in the act of trying to solve the following innocent little arithmetical puzzle. A race between a man and a woman that I happened to witness one All Fools' Day has fixed itself indelibly on my memory. It happened at a country-house, where the gardener and the cook decided to run a race to a point `100` feet straight away and return. I found that the gardener ran `3` feet at every bound and the cook only `2` feet, but then she made three bounds to his two. Now, what was the result of the race?"

    A fortnight after publication I added the following note: "It has been suggested that perhaps there is a catch in the 'return,' but there is not. The race is to a point `100` feet away and home again—that is, a distance of `200` feet. One correspondent asks whether they take exactly the same time in turning, to which I reply that they do. Another seems to suspect that it is really a conundrum, and that the answer is that 'the result of the race was a (matrimonial) tie.' But I had no such intention. The puzzle is an arithmetical one, as it purports to be."

    Sources:

  • Question

    One-seventh of mathematicians are philosophers, and one-ninth of philosophers are mathematicians. Which are there more of – philosophers or mathematicians?

    Sources:

  • Question

    The journey from home to school takes Yossi `20` minutes. One day, when Yossi was already on his way to school, he remembered that he had forgotten his pen at home. If he continues to school now, he will arrive `3` minutes before the bell. And if he goes back home to get the pen, he will be `7 ` minutes late for class. What fraction of the way to school had Yossi traveled when he remembered that he didn't have a pen?

    Note: Yossi walks at a constant speed the entire time.

    Sources:

  • Question

    How can you divide `7` apples equally among `12` children, if you are not allowed to cut any apple into more than `5` pieces?

    Sources:

  • Question

    The sum of several numbers is equal to `1`. Is it possible that the sum of their squares is less than one-tenth?

    Sources: