Arithmetic
Arithmetic is the fundamental branch of mathematics dealing with numbers and the basic operations: addition, subtraction, multiplication, and division. Questions involve performing these operations, understanding number properties (like integers, fractions, decimals), and solving related word problems.
Fractions Percentages Division with Remainder-
THE EIGHT VILLAS
In one of the outlying suburbs of London a man had a square plot of ground on which he decided to build eight villas, as shown in the illustration, with a common recreation ground in the middle. After the houses were completed, and all or some of them let, he discovered that the number of occupants in the three houses forming a side of the square was in every case nine. He did not state how the occupants were distributed, but I have shown by the numbers on the sides of the houses one way in which it might have happened. The puzzle is to discover the total number of ways in which all or any of the houses might be occupied, so that there should be nine persons on each side. In order that there may be no misunderstanding, I will explain that although B is what we call a reflection of A, these would count as two different arrangements, while C, if it is turned round, will give four arrangements; and if turned round in front of a mirror, four other arrangements. All eight must be counted. Sources:
Sources:
- Amusements in Mathematics, Henry Ernest Dudeney Question 276
-
A DORMITORY PUZZLE
In a certain convent there were eight large dormitories on one floor, approached by a spiral staircase in the centre, as shown in our plan. On an inspection one Monday by the abbess it was found that the south aspect was so much preferred that six times as many nuns slept on the south side as on each of the other three sides. She objected to this overcrowding, and ordered that it should be reduced. On Tuesday she found that five times as many slept on the south side as on each of the other sides. Again she complained. On Wednesday she found four times as many on the south side, on Thursday three times as many, and on Friday twice as many. Urging the nuns to further efforts, she was pleased to find on Saturday that an equal number slept on each of the four sides of the house. What is the smallest number of nuns there could have been, and how might they have arranged themselves on each of the six nights? No room may ever be unoccupied.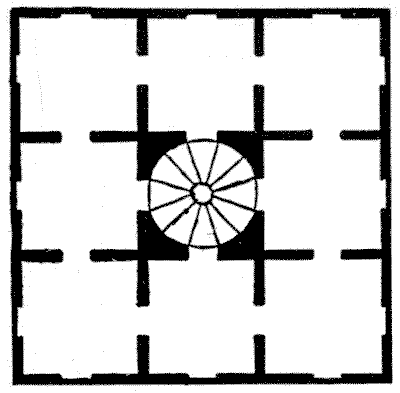 Sources:
Sources:
- Amusements in Mathematics, Henry Ernest Dudeney Question 278
-
MIXING THE TEA
"Mrs. Spooner called this morning," said the honest grocer to his assistant. "She wants twenty pounds of tea at `2`s. `4`½d. per lb. Of course we have a good `2`s. `6`d. tea, a slightly inferior at `2`s. `3`d., and a cheap Indian at `1`s. `9`d., but she is very particular always about her prices."
"What do you propose to do?" asked the innocent assistant.
"Do?" exclaimed the grocer. "Why, just mix up the three teas in different proportions so that the twenty pounds will work out fairly at the lady's price. Only don't put in more of the best tea than you can help, as we make less profit on that, and of course you will use only our complete pound packets. Don't do any weighing."
How was the poor fellow to mix the three teas? Could you have shown him how to do it?
Sources:- Amusements in Mathematics, Henry Ernest Dudeney Question 369
-
A PACKING PUZZLE
As we all know by experience, considerable ingenuity is often required in packing articles into a box if space is not to be unduly wasted. A man once told me that he had a large number of iron balls, all exactly two inches in diameter, and he wished to pack as many of these as possible into a rectangular box `24` `9/10` inches long, `22` `4/5` inches wide, and `14` inches deep. Now, what is the greatest number of the balls that he could pack into that box?Sources:Topics:Geometry -> Solid Geometry / Geometry in Space Arithmetic Minimum and Maximum Problems / Optimization Problems- Amusements in Mathematics, Henry Ernest Dudeney Question 370
-
GOLD PACKING IN RUSSIA
The editor of the Times newspaper was invited by a high Russian official to inspect the gold stored in reserve at St. Petersburg, in order that he might satisfy himself that it was not another "Humbert safe." He replied that it would be of no use whatever, for although the gold might appear to be there, he would be quite unable from a mere inspection to declare that what he saw was really gold. A correspondent of the Daily Mail thereupon took up the challenge, but, although he was greatly impressed by what he saw, he was compelled to confess his incompetence (without emptying and counting the contents of every box and sack, and assaying every piece of gold) to give any assurance on the subject. In presenting the following little puzzle, I wish it to be also understood that I do not guarantee the real existence of the gold, and the point is not at all material to our purpose. Moreover, if the reader says that gold is not usually "put up" in slabs of the dimensions that I give, I can only claim problematic licence.
Russian officials were engaged in packing `800` gold slabs, each measuring `12`½ inches long, `11` inches wide, and `1` inch deep. What are the interior dimensions of a box of equal length and width, and necessary depth, that will exactly contain them without any space being left over? Not more than twelve slabs may be laid on edge, according to the rules of the government. It is an interesting little problem in packing, and not at all difficult.
Sources:- Amusements in Mathematics, Henry Ernest Dudeney Question 371
-
THE DOMINO FRAME PUZZLE
 It will be seen in the illustration that the full set of twenty-eight dominoes is arranged in the form of a square frame, with `6` against `6, 2` against `2`, blank against blank, and so on, as in the game. It will be found that the pips in the top row and left-hand column both add up `44`. The pips in the other two sides sum to `59` and `32` respectively. The puzzle is to rearrange the dominoes in the same form so that all of the four sides shall sum to `44`. Remember that the dominoes must be correctly placed one against another as in the game.
Sources:
It will be seen in the illustration that the full set of twenty-eight dominoes is arranged in the form of a square frame, with `6` against `6, 2` against `2`, blank against blank, and so on, as in the game. It will be found that the pips in the top row and left-hand column both add up `44`. The pips in the other two sides sum to `59` and `32` respectively. The puzzle is to rearrange the dominoes in the same form so that all of the four sides shall sum to `44`. Remember that the dominoes must be correctly placed one against another as in the game.
Sources:
- Amusements in Mathematics, Henry Ernest Dudeney Question 380
-
THE CARD FRAME PUZZLE
In the illustration we have a frame constructed from the ten playing cards, ace to ten of diamonds. The children who made it wanted the pips on all four sides to add up alike, but they failed in their attempt and gave it up as impossible. It will be seen that the pips in the top row, the bottom row, and the left-hand side all add up `14`, but the right-hand side sums to `23`. Now, what they were trying to do is quite possible. Can you rearrange the ten cards in the same formation so that all four sides shall add up alike? Of course they need not add up `14`, but any number you choose to select.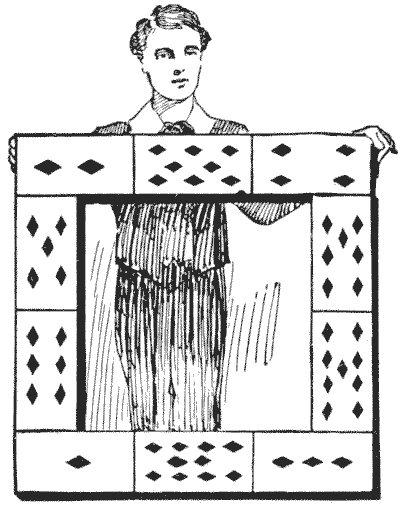 Sources:Topics:Arithmetic Algebra -> Equations Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures
Sources:Topics:Arithmetic Algebra -> Equations Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures- Amusements in Mathematics, Henry Ernest Dudeney Question 381
-
CARD TRIANGLES
Here you pick out the nine cards, ace to nine of diamonds, and arrange them in the form of a triangle, exactly as shown in the illustration, so that the pips add up the same on the three sides. In the example given it will be seen that they sum to `20` on each side, but the particular number is of no importance so long as it is the same on all three sides. The puzzle is to find out in just how many different ways this can be done.
If you simply turn the cards round so that one of the other two sides is nearest to you this will not count as different, for the order will be the same. Also, if you make the `4, 9, 5` change places with the `7, 3, 8`, and at the same time exchange the `1` and the `6`, it will not be different. But if you only change the `1` and the `6` it will be different, because the order round the triangle is not the same. This explanation will prevent any doubt arising as to the conditions.
Sources: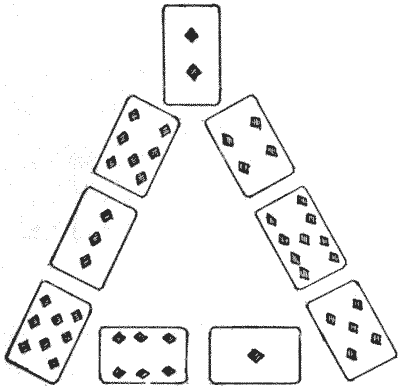
- Amusements in Mathematics, Henry Ernest Dudeney Question 384
-
A TRICK WITH DICE
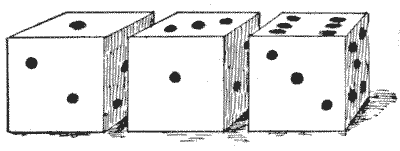 Here is a neat little trick with three dice. I ask you to throw the dice without my seeing them. Then I tell you to multiply the points of the first die by `2` and add `5`; then multiply the result by `5` and add the points of the second die; then multiply the result by `10` and add the points of the third die. You then give me the total, and I can at once tell you the points thrown with the three dice. How do I do it? As an example, if you threw `1, 3`, and `6`, as in the illustration, the result you would give me would be `386`, from which I could at once say what you had thrown.
Sources:
Here is a neat little trick with three dice. I ask you to throw the dice without my seeing them. Then I tell you to multiply the points of the first die by `2` and add `5`; then multiply the result by `5` and add the points of the second die; then multiply the result by `10` and add the points of the third die. You then give me the total, and I can at once tell you the points thrown with the three dice. How do I do it? As an example, if you threw `1, 3`, and `6`, as in the illustration, the result you would give me would be `386`, from which I could at once say what you had thrown.
Sources:
- Amusements in Mathematics, Henry Ernest Dudeney Question 386
-
THE MAGIC STRIPS

I happened to have lying on my table a number of strips of cardboard, with numbers printed on them from `1` upwards in numerical order. The idea suddenly came to me, as ideas have a way of unexpectedly coming, to make a little puzzle of this. I wonder whether many readers will arrive at the same solution that I did.
Take seven strips of cardboard and lay them together as above. Then write on each of them the numbers `1, 2, 3, 4, 5, 6, 7`, as shown, so that the numbers shall form seven rows and seven columns.
Now, the puzzle is to cut these strips into the fewest possible pieces so that they may be placed together and form a magic square, the seven rows, seven columns, and two diagonals adding up the same number. No figures may be turned upside down or placed on their sides—that is, all the strips must lie in their original direction.
Of course you could cut each strip into seven separate pieces, each piece containing a number, and the puzzle would then be very easy, but I need hardly say that forty-nine pieces is a long way from being the fewest possible.
Sources:- Amusements in Mathematics, Henry Ernest Dudeney Question 400