Algebra
Algebra is a broad branch of mathematics that uses symbols (usually letters) to represent numbers and to state rules and relationships. It involves manipulating expressions, solving equations and inequalities, and studying functions and structures. Questions cover a wide range of these topics.
Algebraic Techniques Equations Inequalities Word Problems Sequences-
CROSSING THE STREAM
During a country ramble Mr. and Mrs. Softleigh found themselves in a pretty little dilemma. They had to cross a stream in a small boat which was capable of carrying only `150` lbs. weight. But Mr. Softleigh and his wife each weighed exactly `150` lbs., and each of their sons weighed `75` lbs. And then there was the dog, who could not be induced on any terms to swim. On the principle of "ladies first," they at once sent Mrs. Softleigh over; but this was a stupid oversight, because she had to come back again with the boat, so nothing was gained by that operation. How did they all succeed in getting across? The reader will find it much easier than the Softleigh family did, for their greatest enemy could not have truthfully called them a brilliant quartette—while the dog was a perfect fool.Sources:Topics:Algebra -> Word Problems Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures- Amusements in Mathematics, Henry Ernest Dudeney Question 373
-
CROSSING THE RIVER AXE
 Many years ago, in the days of the smuggler known as "Rob Roy of the West," a piratical band buried on the coast of South Devon a quantity of treasure which was, of course, abandoned by them in the usual inexplicable way. Some time afterwards its whereabouts was discovered by three countrymen, who visited the spot one night and divided the spoil between them, Giles taking treasure to the value of £`800`, Jasper £`500` worth, and Timothy £`300` worth. In returning they had to cross the river Axe at a point where they had left a small boat in readiness. Here, however, was a difficulty they had not anticipated. The boat would only carry two men, or one man and a sack, and they had so little confidence in one another that no person could be left alone on the land or in the boat with more than his share of the spoil, though two persons (being a check on each other) might be left with more than their shares. The puzzle is to show how they got over the river in the fewest possible crossings, taking their treasure with them. No tricks, such as ropes, "flying bridges," currents, swimming, or similar dodges, may be employed.
Sources:Topics:Algebra -> Word Problems Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures
Many years ago, in the days of the smuggler known as "Rob Roy of the West," a piratical band buried on the coast of South Devon a quantity of treasure which was, of course, abandoned by them in the usual inexplicable way. Some time afterwards its whereabouts was discovered by three countrymen, who visited the spot one night and divided the spoil between them, Giles taking treasure to the value of £`800`, Jasper £`500` worth, and Timothy £`300` worth. In returning they had to cross the river Axe at a point where they had left a small boat in readiness. Here, however, was a difficulty they had not anticipated. The boat would only carry two men, or one man and a sack, and they had so little confidence in one another that no person could be left alone on the land or in the boat with more than his share of the spoil, though two persons (being a check on each other) might be left with more than their shares. The puzzle is to show how they got over the river in the fewest possible crossings, taking their treasure with them. No tricks, such as ropes, "flying bridges," currents, swimming, or similar dodges, may be employed.
Sources:Topics:Algebra -> Word Problems Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures- Amusements in Mathematics, Henry Ernest Dudeney Question 374
-
STEALING THE CASTLE TREASURE
The ingenious manner in which a box of treasure, consisting principally of jewels and precious stones, was stolen from Gloomhurst Castle has been handed down as a tradition in the De Gourney family. The thieves consisted of a man, a youth, and a small boy, whose only mode of escape with the box of treasure was by means of a high window. Outside the window was fixed a pulley, over which ran a rope with a basket at each end. When one basket was on the ground the other was at the window. The rope was so disposed that the persons in the basket could neither help themselves by means of it nor receive help from others. In short, the only way the baskets could be used was by placing a heavier weight in one than in the other.
Now, the man weighed `195` lbs., the youth `105` lbs., the boy `90` lbs., and the box of treasure `75` lbs. The weight in the descending basket could not exceed that in the other by more than `15` lbs. without causing a descent so rapid as to be most dangerous to a human being, though it would not injure the stolen property. Only two persons, or one person and the treasure, could be placed in the same basket at one time. How did they all manage to escape and take the box of treasure with them?
The puzzle is to find the shortest way of performing the feat, which in itself is not difficult. Remember, a person cannot help himself by hanging on to the rope, the only way being to go down "with a bump," with the weight in the other basket as a counterpoise.
Sources:Topics:Algebra -> Word Problems Algorithm Theory -> Weighing Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Minimum and Maximum Problems / Optimization Problems- Amusements in Mathematics, Henry Ernest Dudeney Question 377
-
DOMINOES IN PROGRESSION
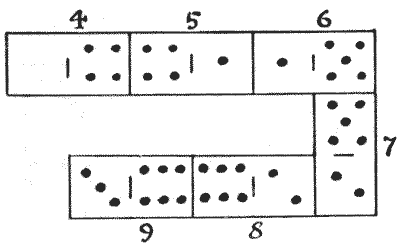 It will be seen that I have played six dominoes, in the illustration, in accordance with the ordinary rules of the game, `4` against `4, 1` against `1`, and so on, and yet the sum of the spots on the successive dominoes, `4, 5, 6, 7, 8, 9`, are in arithmetical progression; that is, the numbers taken in order have a common difference of `1`. In how many different ways may we play six dominoes, from an ordinary box of twenty-eight, so that the numbers on them may lie in arithmetical progression? We must always play from left to right, and numbers in decreasing arithmetical progression (such as `9, 8, 7, 6, 5, 4`) are not admissible.
Sources:Topics:Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures
It will be seen that I have played six dominoes, in the illustration, in accordance with the ordinary rules of the game, `4` against `4, 1` against `1`, and so on, and yet the sum of the spots on the successive dominoes, `4, 5, 6, 7, 8, 9`, are in arithmetical progression; that is, the numbers taken in order have a common difference of `1`. In how many different ways may we play six dominoes, from an ordinary box of twenty-eight, so that the numbers on them may lie in arithmetical progression? We must always play from left to right, and numbers in decreasing arithmetical progression (such as `9, 8, 7, 6, 5, 4`) are not admissible.
Sources:Topics:Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures- Amusements in Mathematics, Henry Ernest Dudeney Question 378
-
THE CARD FRAME PUZZLE
In the illustration we have a frame constructed from the ten playing cards, ace to ten of diamonds. The children who made it wanted the pips on all four sides to add up alike, but they failed in their attempt and gave it up as impossible. It will be seen that the pips in the top row, the bottom row, and the left-hand side all add up `14`, but the right-hand side sums to `23`. Now, what they were trying to do is quite possible. Can you rearrange the ten cards in the same formation so that all four sides shall add up alike? Of course they need not add up `14`, but any number you choose to select.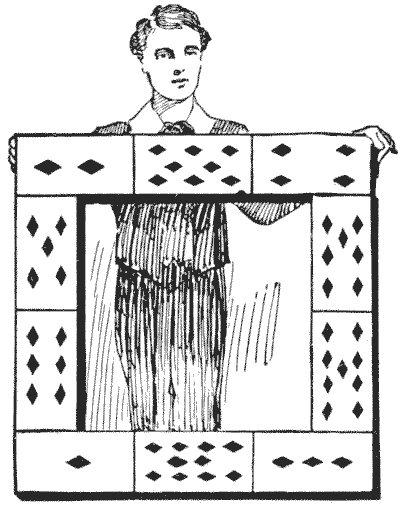 Sources:Topics:Arithmetic Algebra -> Equations Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures
Sources:Topics:Arithmetic Algebra -> Equations Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures- Amusements in Mathematics, Henry Ernest Dudeney Question 381
-
A TRICK WITH DICE
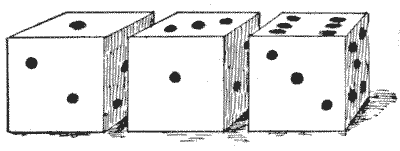 Here is a neat little trick with three dice. I ask you to throw the dice without my seeing them. Then I tell you to multiply the points of the first die by `2` and add `5`; then multiply the result by `5` and add the points of the second die; then multiply the result by `10` and add the points of the third die. You then give me the total, and I can at once tell you the points thrown with the three dice. How do I do it? As an example, if you threw `1, 3`, and `6`, as in the illustration, the result you would give me would be `386`, from which I could at once say what you had thrown.
Sources:
Here is a neat little trick with three dice. I ask you to throw the dice without my seeing them. Then I tell you to multiply the points of the first die by `2` and add `5`; then multiply the result by `5` and add the points of the second die; then multiply the result by `10` and add the points of the third die. You then give me the total, and I can at once tell you the points thrown with the three dice. How do I do it? As an example, if you threw `1, 3`, and `6`, as in the illustration, the result you would give me would be `386`, from which I could at once say what you had thrown.
Sources:
- Amusements in Mathematics, Henry Ernest Dudeney Question 386
-
THE VILLAGE CRICKET MATCH
In a cricket match, Dingley Dell v. All Muggleton, the latter had the first innings. Mr. Dumkins and Mr. Podder were at the wickets, when the wary Dumkins made a splendid late cut, and Mr. Podder called on him to run. Four runs were apparently completed, but the vigilant umpires at each end called, "three short," making six short runs in all. What number did Mr. Dumkins score? When Dingley Dell took their turn at the wickets their champions were Mr. Luffey and Mr. Struggles. The latter made a magnificent off-drive, and invited his colleague to "come along," with the result that the observant spectators applauded them for what was supposed to have been three sharp runs. But the umpires declared that there had been two short runs at each end—four in all. To what extent, if any, did this manœuvre increase Mr. Struggles's total? Sources:- Amusements in Mathematics, Henry Ernest Dudeney Question 387
-
SLOW CRICKET
In the recent county match between Wessex and Nincomshire the former team were at the wickets all day, the last man being put out a few minutes before the time for drawing stumps. The play was so slow that most of the spectators were fast asleep, and, on being awakened by one of the officials clearing the ground, we learnt that two men had been put out leg-before-wicket for a combined score of `19` runs; four men were caught for a combined score or `17` runs; one man was run out for a duck's egg; and the others were all bowled for `3` runs each. There were no extras. We were not told which of the men was the captain, but he made exactly `15` more than the average of his team. What was the captain's score? Sources:- Amusements in Mathematics, Henry Ernest Dudeney Question 388
-
THE HORSE-RACE PUZZLE
There are no morals in puzzles. When we are solving the old puzzle of the captain who, having to throw half his crew overboard in a storm, arranged to draw lots, but so placed the men that only the Turks were sacrificed, and all the Christians left on board, we do not stop to discuss the questionable morality of the proceeding. And when we are dealing with a measuring problem, in which certain thirsty pilgrims are to make an equitable division of a barrel of beer, we do not object that, as total abstainers, it is against our conscience to have anything to do with intoxicating liquor. Therefore I make no apology for introducing a puzzle that deals with betting.
Three horses—Acorn, Bluebottle, and Capsule—start in a race. The odds are `4` to `1`, Acorn; `3` to `1`, Bluebottle; `2` to `1`, Capsule. Now, how much must I invest on each horse in order to win £`13`, no matter which horse comes in first? Supposing, as an example, that I betted £`5` on each horse. Then, if Acorn won, I should receive £`20` (four times £`5`), and have to pay £`5` each for the other two horses; thereby winning £`10`. But it will be found that if Bluebottle was first I should only win £`5`, and if Capsule won I should gain nothing and lose nothing. This will make the question perfectly clear to the novice, who, like myself, is not interested in the calling of the fraternity who profess to be engaged in the noble task of "improving the breed of horses."
Sources:- Amusements in Mathematics, Henry Ernest Dudeney Question 390
-
THE MOTOR-CAR RACE
Sometimes a quite simple statement of fact, if worded in an unfamiliar manner, will cause considerable perplexity. Here is an example, and it will doubtless puzzle some of my more youthful readers just a little. I happened to be at a motor-car race at Brooklands, when one spectator said to another, while a number of cars were whirling round and round the circular track:—
"There's Gogglesmith—that man in the white car!"
"Yes, I see," was the reply; "but how many cars are running in this race?"
Then came this curious rejoinder:—
"One-third of the cars in front of Gogglesmith added to three-quarters of those behind him will give you the answer."
Now, can you tell how many cars were running in the race?
Sources:- Amusements in Mathematics, Henry Ernest Dudeney Question 391