Algebra

Algebra is a broad branch of mathematics that uses symbols (usually letters) to represent numbers and to state rules and relationships. It involves manipulating expressions, solving equations and inequalities, and studying functions and structures. Questions cover a wide range of these topics.

Algebraic Techniques Equations Inequalities Word Problems Sequences

  • CHANGING PLACES

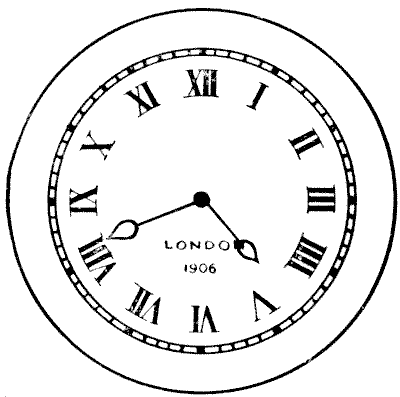    The above clock face indicates a little before `42` minutes past `4`. The hands will again point at exactly the same spots a little after `23` minutes past `8`. In fact, the hands will have changed places. How many times do the hands of a clock change places between three o'clock p.m. and midnight? And out of all the pairs of times indicated by these changes, what is the exact time when the minute hand will be nearest to the point IX? Sources:

  • THE CLUB CLOCK

    One of the big clocks in the Cogitators' Club was found the other night to have stopped just when, as will be seen in the illustration, the second hand was exactly midway between the other two hands. One of the members proposed to some of his friends that they should tell him the exact time when (if the clock had not stopped) the second hand would next again have been midway between the minute hand and the hour hand. Can you find the correct time that it would happen? Sources:

  • THE STOP-WATCH

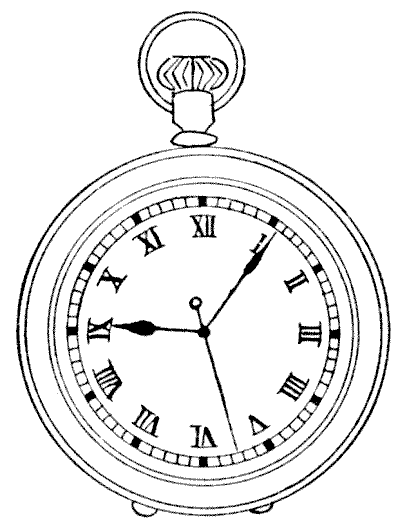    We have here a stop-watch with three hands. The second hand, which travels once round the face in a minute, is the one with the little ring at its end near the centre. Our dial indicates the exact time when its owner stopped the watch. You will notice that the three hands are nearly equidistant. The hour and minute hands point to spots that are exactly a third of the circumference apart, but the second hand is a little too advanced. An exact equidistance for the three hands is not possible. Now, we want to know what the time will be when the three hands are next at exactly the same distances as shown from one another. Can you state the time? Sources:

  • THE THREE CLOCKS

    On Friday, April `1, 1898`, three new clocks were all set going precisely at the same time—twelve noon. At noon on the following day it was found that clock A had kept perfect time, that clock B had gained exactly one minute, and that clock C had lost exactly one minute. Now, supposing that the clocks B and C had not been regulated, but all three allowed to go on as they had begun, and that they maintained the same rates of progress without stopping, on what date and at what time of day would all three pairs of hands again point at the same moment at twelve o'clock? Sources:

  • THE RAILWAY STATION CLOCK

    A clock hangs on the wall of a railway station, `71` ft. `9` in. long and `10` ft. `4` in. high. Those are the dimensions of the wall, not of the clock! While waiting for a train we noticed that the hands of the clock were pointing in opposite directions, and were parallel to one of the diagonals of the wall. What was the exact time? Sources:

  • THE VILLAGE SIMPLETON

    A facetious individual who was taking a long walk in the country came upon a yokel sitting on a stile. As the gentleman was not quite sure of his road, he thought he would make inquiries of the local inhabitant; but at the first glance he jumped too hastily to the conclusion that he had dropped on the village idiot. He therefore decided to test the fellow's intelligence by first putting to him the simplest question he could think of, which was, "What day of the week is this, my good man?" The following is the smart answer that he received:—

    "When the day after to-morrow is yesterday, to-day will be as far from Sunday as to-day was from Sunday when the day before yesterday was to-morrow."

    Can the reader say what day of the week it was? It is pretty evident that the countryman was not such a fool as he looked. The gentleman went on his road a puzzled but a wiser man.

    Sources:

  • AVERAGE SPEED

    In a recent motor ride it was found that we had gone at the rate of ten miles an hour, but we did the return journey over the same route, owing to the roads being more clear of traffic, at fifteen miles an hour. What was our average speed? Do not be too hasty in your answer to this simple little question, or it is pretty certain that you will be wrong. Sources:

  • THE TWO TRAINS

    I put this little question to a stationmaster, and his correct answer was so prompt that I am convinced there is no necessity to seek talented railway officials in America or elsewhere.

    Two trains start at the same time, one from London to Liverpool, the other from Liverpool to London. If they arrive at their destinations one hour and four hours respectively after passing one another, how much faster is one train running than the other?

    Sources:

  • THE THREE VILLAGES

    I set out the other day to ride in a motor-car from Acrefield to Butterford, but by mistake I took the road going via Cheesebury, which is nearer Acrefield than Butterford, and is twelve miles to the left of the direct road I should have travelled. After arriving at Butterford I found that I had gone thirty-five miles. What are the three distances between these villages, each being a whole number of miles? I may mention that the three roads are quite straight. Sources:

  • DRAWING HER PENSION

    "Speaking of odd figures," said a gentleman who occupies some post in a Government office, "one of the queerest characters I know is an old lame widow who climbs up a hill every week to draw her pension at the village post office. She crawls up at the rate of a mile and a half an hour and comes down at the rate of four and a half miles an hour, so that it takes her just six hours to make the double journey. Can any of you tell me how far it is from the bottom of the hill to the top?" Sources: