Arithmetic, Fractions

Fractions represent parts of a whole or ratios between numbers. This topic covers understanding, comparing, simplifying, and performing arithmetic operations (addition, subtraction, multiplication, division) with fractions and mixed numbers. Questions often involve practical applications.

  • DOMESTIC ECONOMY

    Young Mrs. Perkins, of Putney, writes to me as follows: "I should be very glad if you could give me the answer to a little sum that has been worrying me a good deal lately. Here it is: We have only been married a short time, and now, at the end of two years from the time when we set up housekeeping, my husband tells me that he finds we have spent a third of his yearly income in rent, rates, and taxes, one-half in domestic expenses, and one-ninth in other ways. He has a balance of £`190` remaining in the bank. I know this last, because he accidentally left out his pass-book the other day, and I peeped into it. Don't you think that a husband ought to give his wife his entire confidence in his money matters? Well, I do; and—will you believe it?—he has never told me what his income really is, and I want, very naturally, to find out. Can you tell me what it is from the figures I have given you?"

    Yes; the answer can certainly be given from the figures contained in Mrs. Perkins's letter. And my readers, if not warned, will be practically unanimous in declaring the income to be—something absurdly in excess of the correct answer!

    Sources:

  • BUYING CHESTNUTS

    Though the following little puzzle deals with the purchase of chestnuts, it is not itself of the "chestnut" type. It is quite new. At first sight it has certainly the appearance of being of the "nonsense puzzle" character, but it is all right when properly considered.

    A man went to a shop to buy chestnuts. He said he wanted a pennyworth, and was given five chestnuts. "It is not enough; I ought to have a sixth," he remarked! "But if I give you one chestnut more." the shopman replied, "you will have five too many." Now, strange to say, they were both right. How many chestnuts should the buyer receive for half a crown?

    Sources:

  • THE BAG OF NUTS

    Three boys were given a bag of nuts as a Christmas present, and it was agreed that they should be divided in proportion to their ages, which together amounted to `17 1/2` years. Now the bag contained `770` nuts, and as often as Herbert took four Robert took three, and as often as Herbert took six Christopher took seven. The puzzle is to find out how many nuts each had, and what were the boys' respective ages.

    Sources:

  • A PUZZLING WATCH

    A friend pulled out his watch and said, "This watch of mine does not keep perfect time; I must have it seen to. I have noticed that the minute hand and the hour hand are exactly together every sixty-five minutes." Does that watch gain or lose, and how much per hour? Sources:

  • THE WAPSHAW'S WHARF MYSTERY

    There was a great commotion in Lower Thames Street on the morning of January `12, 1887`. When the early members of the staff arrived at Wapshaw's Wharf they found that the safe had been broken open, a considerable sum of money removed, and the offices left in great disorder. The night watchman was nowhere to be found, but nobody who had been acquainted with him for one moment suspected him to be guilty of the robbery. In this belief the proprietors were confirmed when, later in the day, they were informed that the poor fellow's body had been picked up by the River Police. Certain marks of violence pointed to the fact that he had been brutally attacked and thrown into the river. A watch found in his pocket had stopped, as is invariably the case in such circumstances, and this was a valuable clue to the time of the outrage. But a very stupid officer (and we invariably find one or two stupid individuals in the most intelligent bodies of men) had actually amused himself by turning the hands round and round, trying to set the watch going again. After he had been severely reprimanded for this serious indiscretion, he was asked whether he could remember the time that was indicated by the watch when found. He replied that he could not, but he recollected that the hour hand and minute hand were exactly together, one above the other, and the second hand had just passed the forty-ninth second. More than this he could not remember.

    What was the exact time at which the watchman's watch stopped? The watch is, of course, assumed to have been an accurate one.

    Sources:

  • THE STOP-WATCH

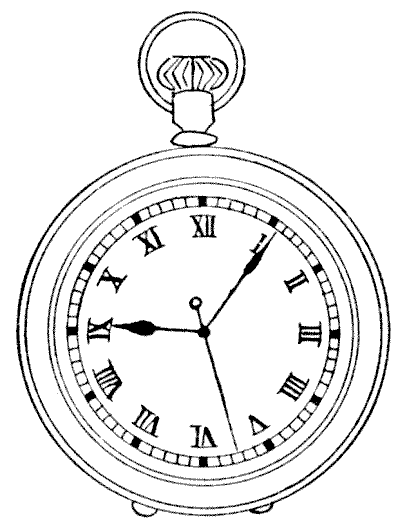    We have here a stop-watch with three hands. The second hand, which travels once round the face in a minute, is the one with the little ring at its end near the centre. Our dial indicates the exact time when its owner stopped the watch. You will notice that the three hands are nearly equidistant. The hour and minute hands point to spots that are exactly a third of the circumference apart, but the second hand is a little too advanced. An exact equidistance for the three hands is not possible. Now, we want to know what the time will be when the three hands are next at exactly the same distances as shown from one another. Can you state the time? Sources:

  • THE RAILWAY STATION CLOCK

    A clock hangs on the wall of a railway station, `71` ft. `9` in. long and `10` ft. `4` in. high. Those are the dimensions of the wall, not of the clock! While waiting for a train we noticed that the hands of the clock were pointing in opposite directions, and were parallel to one of the diagonals of the wall. What was the exact time? Sources:

  • ODD AND EVEN DIGITS

    The odd digits, `1, 3, 5, 7`, and `9`, add up `25`, while the even figures, `2, 4, 6`, and `8`, only add up `20`. Arrange these figures so that the odd ones and the even ones add up alike. Complex and improper fractions and recurring decimals are not allowed.
    Topics:
    Arithmetic -> Fractions
    Sources:

  • THE CENTURY PUZZLE

    Can you write `100` in the form of a mixed number, using all the nine digits once, and only once? The late distinguished French mathematician, Edouard Lucas, found seven different ways of doing it, and expressed his doubts as to there being any other ways. As a matter of fact there are just eleven ways and no more. Here is one of them, `91 5742/638`. Nine of the other ways have similarly two figures in the integral part of the number, but the eleventh expression has only one figure there. Can the reader find this last form?

    Sources:

  • MORE MIXED FRACTIONS

    When I first published my solution to the last puzzle, I was led to attempt the expression of all numbers in turn up to `100` by a mixed fraction containing all the nine digits. Here are twelve numbers for the reader to try his hand at: `13, 14, 15, 16, 18, 20, 27, 36, 40, 69, 72, 94`. Use every one of the nine digits once, and only once, in every case.

    Sources: