Gillis Mathematical Olympiad, 2016-2017
-
Question 1 - Regular Polygons and Circles
A.
In the right-hand figure, there is a square containing 4 circles. The radii of the circles are equal to each other, and each circle is tangent to two other circles and also to two sides of the square. Find the ratio between the area of the blue part and the area of the white part of the square.
B.
In the left-hand figure, there is a hexagon containing 6 circles with the same radius. Each circle is tangent to two other circles and also to one side of the hexagon, at its midpoint. Find the ratio between the area of the blue part and the area of the white part of the hexagon.
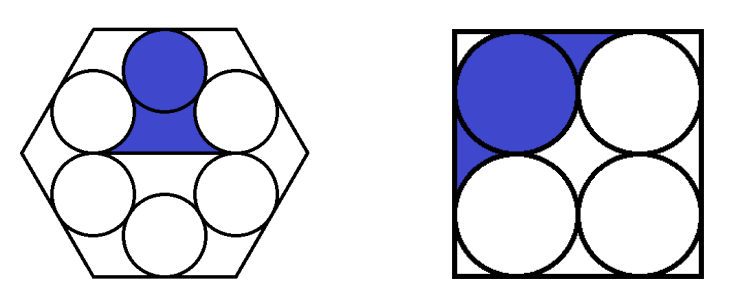
(Solution format: "x, y" for example "1/8, 7/100")
-
Question 2 - Sum of Products of Digits
Let `P(n)` denote the product of the digits of the number `n`. For example, `P(1948) = 1 * 9 * 4 * 8 = 288`.
A.
Calculate `P(1) + P(2) + P(3) + ... + P(2016)`
B.
Find the maximum value of `{P(n)} /n`, where `2016 <= n <= 5777`.
(Solution format: "x, y/z" where y/z is an unreduced fraction. For example "10000, 35/100")
Topics:Arithmetic Algebra -> Word Problems Combinatorics -> Number Tables Number Theory -> Division -
Question 3 - Right Triangles and a Square
Given a large number of congruent right triangles.
The side lengths of each triangle are 3, 4, and 5.
What is the maximum number of such triangles that can be placed inside a 20×20 square, such that they do not overlap?
Topics:Geometry -> Area Calculation Geometry -> Plane Geometry -> Triangles Geometry -> Plane Geometry -> Pythagorean Theorem