Gillis Mathematical Olympiad, 2016-2017
-
问题 1 - 正多边形和圆
A.
在右边的图中,有一个正方形,里面有4个圆。这些圆的半径相等,每个圆与另外两个圆相切,并且与正方形的两条边相切。求正方形中蓝色部分面积与白色部分面积的比率。
B.
在左边的图中,有一个六边形,里面有6个半径相同的圆。每个圆与另外两个圆相切,并且与六边形的一条边在中间位置相切。求六边形中蓝色部分面积与白色部分面积的比率。
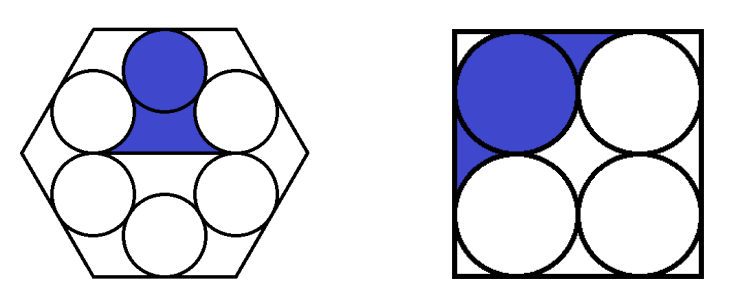
(答案格式:"x, y" 例如 "1/8, 7/100")
-
问题 2 - 数字乘积之和
设 `P(n)` 表示数字 `n` 的各位数字的乘积。例如, `P(1948) = 1 * 9 * 4 * 8 = 288`。
A.
计算 `P(1) + P(2) + P(3) + ... + P(2016)`
B.
找到`{P(n)} /n`的最大值,当 `2016 <= n <= 5777`时。
(解的格式:“x, y/z”,其中 y/z 是一个不可约分的的真分数。例如“10000, 35/100”)
-
问题 3 - 直角三角形和正方形
给定大量全等的直角三角形。
每个三角形的边长分别为 3、4 和 5。
最多可以在 20×20 的正方形内放置多少个这样的三角形,使它们互不重叠?