Number Theory

Number Theory is a branch of mathematics concerned with the properties of integers. Topics include prime numbers, divisibility, congruences (modular arithmetic), Diophantine equations, and functions of integers. Questions often require analytical and creative thinking about numbers.

Prime Numbers Chinese Remainder Theorem Modular Arithmetic / Remainder Arithmetic Greatest Common Divisor (GCD) and Least Common Multiple (LCM) Triangular Numbers Division

• Integer Expression

  Find all integers n for which the expression `{(n+2)^4}/{n-1}` is defined and an integer.

  Show hint

  Log in here to receive the hint
  Topics:

  Number Theory Algebra -> Equations
  Sources:
  • Junior Science Team Exercises, 2024-2025, Assignment 1 Question 6

• The 1224th Digit

  We write the natural numbers in order, one after the other from left to right:

  1234567891011...

  Note, for example, that the digit in the 10th place is 1 and the digit in the 11th place is 0.

  Continuing with this writing as much as needed...

  Which digit will be in the 1224th place in the sequence?

  Topics:

  Number Theory Arithmetic Proof and Example -> Constructing an Example / Counterexample Algebra -> Sequences
  Sources:
  • Bar-Ilan's weekly mathriddle competition, 2024 Question 1

• Polynomial with Integer Coefficients

  Let `p(x)` be a polynomial with integer coefficients such that `p(-2006) < p(2006)=2005`. Prove that `p(-2006)<=-2007`.
   

  Topics:

  Number Theory Algebra -> Algebraic Techniques Algebra -> Inequalities
  Sources:
  • Grossman Math Olympiad, 2006 Question 6

• Question

  Eighth-grade students threw rubber balls into a box and then tried to guess how many balls had accumulated there. Five students tried to guess: 45, 41, 55, 50, 43, but no one guessed the exact amount. The guesses differed from the truth by 3, 7, 5, 7, and 2 balls (not necessarily in the same order as the guesses). How many balls were in the box?

  Topics:

  Number Theory Arithmetic Algebra -> Word Problems Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures
  Sources:
  • Beno Arbel Olympiad, 2017, Grade 8 Question 1

• Question

  In this letter exercise, identical letters represent identical digits, different letters represent different digits, and asterisks represent any digit. Find all the digits.
  `(ABCD)^2 = A B ** ** ** C D `

  Topics:

  Number Theory Arithmetic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Puzzles and Rebuses -> Reconstruct the Exercise / Cryptarithmetic
  Sources:
  • Beno Arbel Olympiad, 2017, Grade 8 Question 4

• THE LOCKERS PUZZLE

   

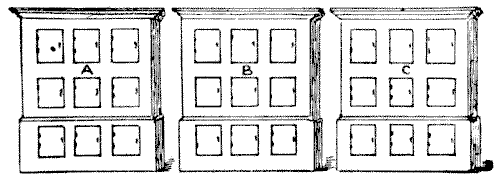
  A man had in his office three cupboards, each containing nine lockers, as shown in the diagram. He told his clerk to place a different one-figure number on each locker of cupboard A, and to do the same in the case of B, and of C. As we are here allowed to call nought a digit, and he was not prohibited from using nought as a number, he clearly had the option of omitting any one of ten digits from each cupboard.

  Now, the employer did not say the lockers were to be numbered in any numerical order, and he was surprised to find, when the work was done, that the figures had apparently been mixed up indiscriminately. Calling upon his clerk for an explanation, the eccentric lad stated that the notion had occurred to him so to arrange the figures that in each case they formed a simple addition sum, the two upper rows of figures producing the sum in the lowest row. But the most surprising point was this: that he had so arranged them that the addition in A gave the smallest possible sum, that the addition in C gave the largest possible sum, and that all the nine digits in the three totals were different. The puzzle is to show how this could be done. No decimals are allowed and the nought may not appear in the hundreds place.

  Topics:

  Number Theory Arithmetic Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 79

• THE THREE GROUPS

  There appeared in "Nouvelles Annales de Mathématiques" the following puzzle as a modification of one of my "Canterbury Puzzles." Arrange the nine digits in three groups of two, three, and four digits, so that the first two numbers when multiplied together make the third. Thus, `12` × `483` = `5,796`. I now also propose to include the cases where there are one, four, and four digits, such as `4` × `1,738` = `6,952`. Can you find all the possible solutions in both cases?
  Topics:

  Number Theory Arithmetic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 80

• DIGITAL MULTIPLICATION

  Here is another entertaining problem with the nine digits, the nought being excluded. Using each figure once, and only once, we can form two multiplication sums that have the same product, and this may be done in many ways. For example, 7x658 and 14x329 contain all the digits once, and the product in each case is the same—`4,606`. Now, it will be seen that the sum of the digits in the product is `16`, which is neither the highest nor the lowest sum so obtainable. Can you find the solution of the problem that gives the lowest possible sum of digits in the common product? Also that which gives the highest possible sum?
  Topics:

  Number Theory Arithmetic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 83

• THE PIERROT'S PUZZLE

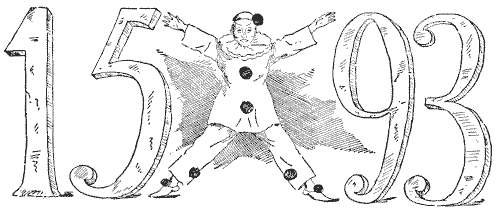  The Pierrot in the illustration is standing in a posture that represents the sign of multiplication. He is indicating the peculiar fact that `15` multiplied by `93` produces exactly the same figures (`1,395`), differently arranged. The puzzle is to take any four digits you like (all different) and similarly arrange them so that the number formed on one side of the Pierrot when multiplied by the number on the other side shall produce the same figures. There are very few ways of doing it, and I shall give all the cases possible. Can you find them all? You are allowed to put two figures on each side of the Pierrot as in the example shown, or to place a single figure on one side and three figures on the other. If we only used three digits instead of four, the only possible ways are these: `3` multiplied by `51` equals `153`, and `6` multiplied by `21` equals `126`.
  Topics:

  Number Theory Arithmetic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 84

• THE NUMBER CHECKS PUZZLE

  Where a large number of workmen are employed on a building it is customary to provide every man with a little disc bearing his number. These are hung on a board by the men as they arrive, and serve as a check on punctuality. Now, I once noticed a foreman remove a number of these checks from his board and place them on a split-ring which he carried in his pocket. This at once gave me the idea for a good puzzle. In fact, I will confide to my readers that this is just how ideas for puzzles arise. You cannot really create an idea: it happens—and you have to be on the alert to seize it when it does so happen.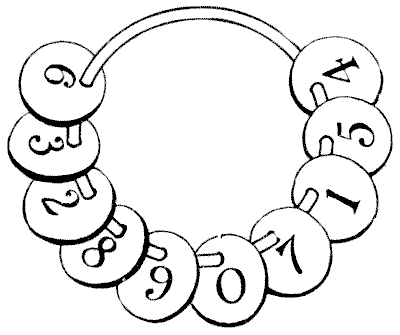 It will be seen from the illustration that there are ten of these checks on a ring, numbered `1` to `9` and `0`. The puzzle is to divide them into three groups without taking any off the ring, so that the first group multiplied by the second makes the third group. For example, we can divide them into the three groups, `2`—`8` `9` `7`—`1` `5` `4` `6` `3`, by bringing the `6` and the `3` round to the `4`, but unfortunately the first two when multiplied together do not make the third. Can you separate them correctly? Of course you may have as many of the checks as you like in any group. The puzzle calls for some ingenuity, unless you have the luck to hit on the answer by chance.
  Topics:

  Number Theory Arithmetic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Puzzles and Rebuses
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 87