Number Theory

Number Theory is a branch of mathematics concerned with the properties of integers. Topics include prime numbers, divisibility, congruences (modular arithmetic), Diophantine equations, and functions of integers. Questions often require analytical and creative thinking about numbers.

Prime Numbers Chinese Remainder Theorem Modular Arithmetic / Remainder Arithmetic Greatest Common Divisor (GCD) and Least Common Multiple (LCM) Triangular Numbers Division

  • MORE MIXED FRACTIONS

    When I first published my solution to the last puzzle, I was led to attempt the expression of all numbers in turn up to `100` by a mixed fraction containing all the nine digits. Here are twelve numbers for the reader to try his hand at: `13, 14, 15, 16, 18, 20, 27, 36, 40, 69, 72, 94`. Use every one of the nine digits once, and only once, in every case.

    Sources:

  • DIGITAL SQUARE NUMBERS

    Here are the nine digits so arranged that they form four square numbers: `9, 81, 324, 576`. Now, can you put them all together so as to form a single square number—(I) the smallest possible, and (II) the largest possible? Sources:

  • THE TORN NUMBER

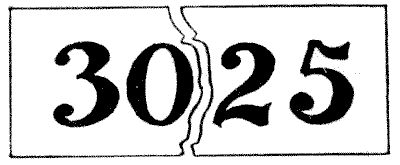
    I had the other day in my possession a label bearing the number `3\ 0\ 2\ 5` in large figures. This got accidentally torn in half, so that `30` was on one piece and `25` on the other, as shown on the illustration. On looking at these pieces I began to make a calculation, scarcely conscious of what I was doing, when I discovered this little peculiarity. If we add the `30` and the `25` together and square the sum we get as the result the complete original number on the label! Thus, `30` added to `25` is `55`, and `55` multiplied by `55` is `3025`. Curious, is it not? Now, the puzzle is to find another number, composed of four figures, all different, which may be divided in the middle and produce the same result.

    Sources:

  • CURIOUS NUMBERS

    The number `48` has this peculiarity, that if you add `1` to it the result is a square number (`49`, the square of `7`), and if you add `1` to its half, you also get a square number (`25`, the square of `5`). Now, there is no limit to the numbers that have this peculiarity, and it is an interesting puzzle to find three more of them—the smallest possible numbers. What are they? Sources:

  • A PRINTER'S ERROR

    In a certain article a printer had to set up the figures `5^4xx2^3`, which, of course, means that the fourth power of `5` (`625`) is to be multiplied by the cube of `2` (`8`), the product of which is `5,000`. But he printed `5^4xx2^3` as `5\ 4\ 2\ 3`, which is not correct. Can you place four digits in the manner shown, so that it will be equally correct if the printer sets it up aright or makes the same blunder?

    Sources:

  • CIRCLING THE SQUARES

     

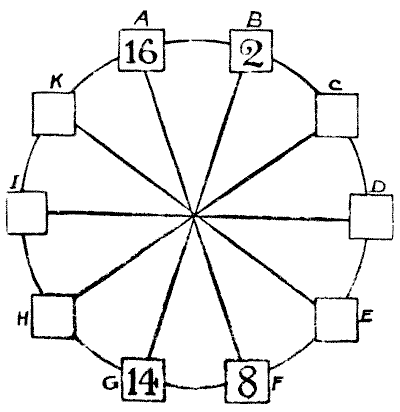
    The puzzle is to place a different number in each of the ten squares so that the sum of the squares of any two adjacent numbers shall be equal to the sum of the squares of the two numbers diametrically opposite to them. The four numbers placed, as examples, must stand as they are. The square of `16` is `256`, and the square of `2` is `4`. Add these together, and the result is `260`. Also—the square of `14` is `196`, and the square of `8` is `64`. These together also make `260`. Now, in precisely the same way, B and C should be equal to G and H (the sum will not necessarily be `260`), A and K to F and E, H and I to C and D, and so on, with any two adjoining squares in the circle.

    All you have to do is to fill in the remaining six numbers. Fractions are not allowed, and I shall show that no number need contain more than two figures.

    Sources:

  • A PROBLEM IN SQUARES

    We possess three square boards. The surface of the first contains five square feet more than the second, and the second contains five square feet more than the third. Can you give exact measurements for the sides of the boards? If you can solve this little puzzle, then try to find three squares in arithmetical progression, with a common difference of `7` and also of `13`. Sources:

  • THE BATTLE OF HASTINGS

    All historians know that there is a great deal of mystery and uncertainty concerning the details of the ever-memorable battle on that fatal day, October `14, 1066`. My puzzle deals with a curious passage in an ancient monkish chronicle that may never receive the attention that it deserves, and if I am unable to vouch for the authenticity of the document it will none the less serve to furnish us with a problem that can hardly fail to interest those of my readers who have arithmetical predilections. Here is the passage in question.

    "The men of Harold stood well together, as their wont was, and formed sixty and one squares, with a like number of men in every square thereof, and woe to the hardy Norman who ventured to enter their redoubts; for a single blow of a Saxon war-hatchet would break his lance and cut through his coat of mail.... When Harold threw himself into the fray the Saxons were one mighty square of men, shouting the battle-cries, 'Ut!' 'Olicrosse!' 'Godemitè!'"

    Now, I find that all the contemporary authorities agree that the Saxons did actually fight in this solid order. For example, in the "Carmen de Bello Hastingensi," a poem attributed to Guy, Bishop of Amiens, living at the time of the battle, we are told that "the Saxons stood fixed in a dense mass," and Henry of Huntingdon records that "they were like unto a castle, impenetrable to the Normans;" while Robert Wace, a century after, tells us the same thing. So in this respect my newly-discovered chronicle may not be greatly in error. But I have reason to believe that there is something wrong with the actual figures. Let the reader see what he can make of them.

    The number of men would be sixty-one times a square number; but when Harold himself joined in the fray they were then able to form one large square. What is the smallest possible number of men there could have been?

    In order to make clear to the reader the simplicity of the question, I will give the lowest solutions in the case of `60` and `62`, the numbers immediately preceding and following `61`. They are `60xx4^2+1 = 31^2`, and `62xx8^2+1=63^2`. That is, `60` squares of `16` men each would be `960` men, and when Harold joined them they would be `961` in number, and so form a square with `31` men on every side. Similarly in the case of the figures I have given for `62`. Now, find the lowest answer for `61`.

    Sources:

  • THE SCULPTOR'S PROBLEM

    An ancient sculptor was commissioned to supply two statues, each on a cubical pedestal. It is with these pedestals that we are concerned. They were of unequal sizes, as will be seen in the illustration, and when the time arrived for payment a dispute arose as to whether the agreement was based on lineal or cubical measurement. But as soon as they came to measure the two pedestals the matter was at once settled, because, curiously enough, the number of lineal feet was exactly the same as the number of cubical feet. The puzzle is to find the dimensions for two pedestals having this peculiarity, in the smallest possible figures. You see, if the two pedestals, for example, measure respectively `3` ft. and `1` ft. on every side, then the lineal measurement would be `4` ft. and the cubical contents `28` ft., which are not the same, so these measurements will not do. Sources:

  • THE SPANISH MISER

    There once lived in a small town in New Castile a noted miser named Don Manuel Rodriguez. His love of money was only equalled by a strong passion for arithmetical problems. These puzzles usually dealt in some way or other with his accumulated treasure, and were propounded by him solely in order that he might have the pleasure of solving them himself. Unfortunately very few of them have survived, and when travelling through Spain, collecting material for a proposed work on "The Spanish Onion as a Cause of National Decadence," I only discovered a very few. One of these concerns the three boxes that appear in the accompanying authentic portrait. Each box contained a different number of golden doubloons. The difference between the number of doubloons in the upper box and the number in the middle box was the same as the difference between the number in the middle box and the number in the bottom box. And if the contents of any two of the boxes were united they would form a square number. What is the smallest number of doubloons that there could have been in any one of the boxes? Sources: