Number Theory
Number Theory is a branch of mathematics concerned with the properties of integers. Topics include prime numbers, divisibility, congruences (modular arithmetic), Diophantine equations, and functions of integers. Questions often require analytical and creative thinking about numbers.
Prime Numbers Chinese Remainder Theorem Modular Arithmetic / Remainder Arithmetic Greatest Common Divisor (GCD) and Least Common Multiple (LCM) Triangular Numbers Division-
MAGIC SQUARES OF TWO DEGREES
While reading a French mathematical work I happened to come across, the following statement: "A very remarkable magic square of `8`, in two degrees, has been constructed by M. Pfeffermann. In other words, he has managed to dispose the sixty-four first numbers on the squares of a chessboard in such a way that the sum of the numbers in every line, every column, and in each of the two diagonals, shall be the same; and more, that if one substitutes for all the numbers their squares, the square still remains magic." I at once set to work to solve this problem, and, although it proved a very hard nut, one was rewarded by the discovery of some curious and beautiful laws that govern it. The reader may like to try his hand at the puzzle.
Sources:- Amusements in Mathematics, Henry Ernest Dudeney Question 408
-
THE BASKETS OF PLUMS
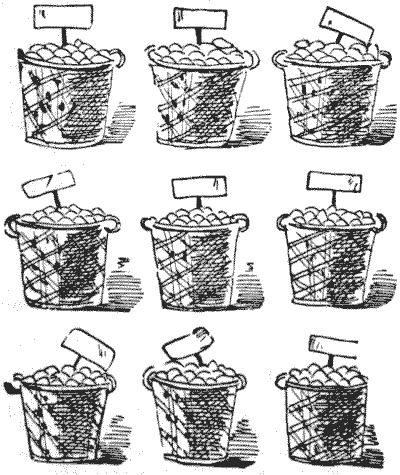
This is the form in which I first introduced the question of magic squares with prime numbers. I will here warn the reader that there is a little trap.
A fruit merchant had nine baskets. Every basket contained plums (all sound and ripe), and the number in every basket was different. When placed as shown in the illustration they formed a magic square, so that if he took any three baskets in a line in the eight possible directions there would always be the same number of plums. This part of the puzzle is easy enough to understand. But what follows seems at first sight a little queer.
The merchant told one of his men to distribute the contents of any basket he chose among some children, giving plums to every child so that each should receive an equal number. But the man found it quite impossible, no matter which basket he selected and no matter how many children he included in the treat. Show, by giving contents of the nine baskets, how this could come about.
Sources:- Amusements in Mathematics, Henry Ernest Dudeney Question 409
-
THE MANDARIN'S "T" PUZZLE
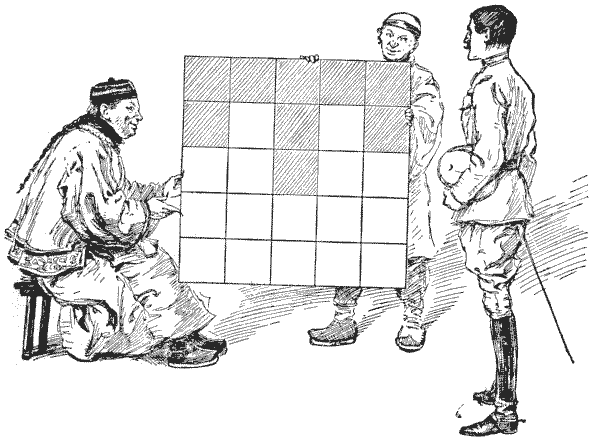
Before Mr. Beauchamp Cholmondely Marjoribanks set out on his tour in the Far East, he prided himself on his knowledge of magic squares, a subject that he had made his special hobby; but he soon discovered that he had never really touched more than the fringe of the subject, and that the wily Chinee could beat him easily. I present a little problem that one learned mandarin propounded to our traveller, as depicted on the last page.
The Chinaman, after remarking that the construction of the ordinary magic square of twenty-five cells is "too velly muchee easy," asked our countryman so to place the numbers `1` to `25` in the square that every column, every row, and each of the two diagonals should add up `65`, with only prime numbers on the shaded "T." Of course the prime numbers available are `1, 2, 3, 5, 7, 11, 13, 17, 19`, and `23`, so you are at liberty to select any nine of these that will serve your purpose. Can you construct this curious little magic square?
Sources:- Amusements in Mathematics, Henry Ernest Dudeney Question 410
-
A MAGIC SQUARE OF COMPOSITES
As we have just discussed the construction of magic squares with prime numbers, the following forms an interesting companion problem. Make a magic square with nine consecutive composite numbers—the smallest possible.Sources:Topics:Number Theory -> Prime Numbers- Amusements in Mathematics, Henry Ernest Dudeney Question 411
-
Question
A grasshopper can jump `80` centimeters forward or `50` centimeters backward. Can the grasshopper move away from its starting point in fewer than `7` jumps to a distance of exactly one meter and `70` cm?
-
Question
Prove that there exist two powers of `2` such that their difference is divisible by `2017`.
Sources: -
Question
Given a positive integer N, consider the following process: Let `S(N)` denote the sum of the digits of N. Take the sum of the digits of `S(N)`. Repeat this operation until a single-digit number is obtained. We call the number of times we performed the above process until we obtained a single-digit number the "depth" of N. For example, the depth of 49 is `S(49)=13 -> S(13)=4`, the operation was performed twice (and the depth of 45 is 1).
a) Prove that for every number N there is indeed a finite depth, that is, a single-digit number is always obtained at some stage of the process.
b) Let `x(n)` denote the minimum number (with the smallest value) with depth N. Find the remainder of `x(5776)` when divided by 6. Justify your answer!
c) Find the remainder of the number `x(5776) - x(5708)` when divided by 2016. Justify your answer!
Sources:Topics:Number Theory -> Modular Arithmetic / Remainder Arithmetic Combinatorics -> Induction (Mathematical Induction) Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence- Gillis Mathematical Olympiad, 2015-2016 Question 3
-
Question
Prove that among five integers, it is possible to choose two whose difference is divisible by `4`.
-
Question
The numbers from `1` to `2n` are written in a row in some order. Add to each number the index of the position it stands on. Prove that among the `2n` sums we obtained, there are two whose difference is divisible by `2n`.
-
777
What is the last digit of the number `777^777`?