Logic

Logic is the study of reasoning and valid inference. It involves analyzing statements, arguments, and deductive processes. Questions may include solving logic puzzles, evaluating the truth of compound statements, using truth tables, and identifying logical fallacies.

Reasoning / Logic Truth-tellers and Liars Problems

  • THE SABBATH PUZZLE

    I have come across the following little poser in an old book. I wonder how many readers will see the author's intended solution to the riddle. 

    Christians the week's first day for Sabbath hold;
    The Jews the seventh, as they did of old;
    The Turks the sixth, as we have oft been told.
    How can these three, in the same place and day,
    Have each his own true Sabbath? tell, I pray.

    Sources:

  • THE RUBY BROOCH

    The annals of Scotland Yard contain some remarkable cases of jewel robberies, but one of the most perplexing was the theft of Lady Littlewood's rubies. There have, of course, been many greater robberies in point of value, but few so artfully conceived. Lady Littlewood, of Romley Manor, had a beautiful but rather eccentric heirloom in the form of a ruby brooch. While staying at her town house early in the eighties she took the jewel to a shop in Brompton for some slight repairs.

    "A fine collection of rubies, madam," said the shopkeeper, to whom her ladyship was a stranger.

    "Yes," she replied; "but curiously enough I have never actually counted them. My mother once pointed out to me that if you start from the centre and count up one line, along the outside and down the next line, there are always eight rubies. So I should always know if a stone were missing."

     

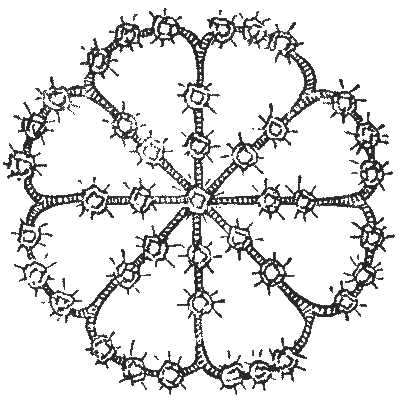
    Six months later a brother of Lady Littlewood's, who had returned from his regiment in India, noticed that his sister was wearing the ruby brooch one night at a county ball, and on their return home asked to look at it more closely. He immediately detected the fact that four of the stones were gone.

    "How can that possibly be?" said Lady Littlewood. "If you count up one line from the centre, along the edge, and down the next line, in any direction, there are always eight stones. This was always so and is so now. How, therefore, would it be possible to remove a stone without my detecting it?"

    "Nothing could be simpler," replied the brother. "I know the brooch well. It originally contained forty-five stones, and there are now only forty-one. Somebody has stolen four rubies, and then reset as small a number of the others as possible in such a way that there shall always be eight in any of the directions you have mentioned."

    There was not the slightest doubt that the Brompton jeweller was the thief, and the matter was placed in the hands of the police. But the man was wanted for other robberies, and had left the neighbourhood some time before. To this day he has never been found.

    The interesting little point that at first baffled the police, and which forms the subject of our puzzle, is this: How were the forty-five rubies originally arranged on the brooch? The illustration shows exactly how the forty-one were arranged after it came back from the jeweller; but although they count eight correctly in any of the directions mentioned, there are four stones missing.

    Sources:

  • THE GARDENER AND THE COOK

    A correspondent, signing himself "Simple Simon," suggested that I should give a special catch puzzle in the issue of The Weekly Dispatch for All Fools' Day, `1900`. So I gave the following, and it caused considerable amusement; for out of a very large body of competitors, many quite expert, not a single person solved it, though it ran for nearly a month.

     

    "The illustration is a fancy sketch of my correspondent, 'Simple Simon,' in the act of trying to solve the following innocent little arithmetical puzzle. A race between a man and a woman that I happened to witness one All Fools' Day has fixed itself indelibly on my memory. It happened at a country-house, where the gardener and the cook decided to run a race to a point `100` feet straight away and return. I found that the gardener ran `3` feet at every bound and the cook only `2` feet, but then she made three bounds to his two. Now, what was the result of the race?"

    A fortnight after publication I added the following note: "It has been suggested that perhaps there is a catch in the 'return,' but there is not. The race is to a point `100` feet away and home again—that is, a distance of `200` feet. One correspondent asks whether they take exactly the same time in turning, to which I reply that they do. Another seems to suspect that it is really a conundrum, and that the answer is that 'the result of the race was a (matrimonial) tie.' But I had no such intention. The puzzle is an arithmetical one, as it purports to be."

    Sources:

  • FIND THE MAN'S WIFE

     

    One summer day in `1903` I was loitering on the Brighton front, watching the people strolling about on the beach, when the friend who was with me suddenly drew my attention to an individual who was standing alone, and said, "Can you point out that man's wife? They are stopping at the same hotel as I am, and the lady is one of those in view." After a few minutes' observation, I was successful in indicating the lady correctly. My friend was curious to know by what method of reasoning I had arrived at the result. This was my answer:—

    "We may at once exclude that Sister of Mercy and the girl in the short frock; also the woman selling oranges. It cannot be the lady in widows' weeds. It is not the lady in the bath chair, because she is not staying at your hotel, for I happened to see her come out of a private house this morning assisted by her maid. The two ladies in red breakfasted at my hotel this morning, and as they were not wearing outdoor dress I conclude they are staying there. It therefore rests between the lady in blue and the one with the green parasol. But the left hand that holds the parasol is, you see, ungloved and bears no wedding-ring. Consequently I am driven to the conclusion that the lady in blue is the man's wife—and you say this is correct."

    Now, as my friend was an artist, and as I thought an amusing puzzle might be devised on the lines of his question, I asked him to make me a drawing according to some directions that I gave him, and I have pleasure in presenting his production to my readers. It will be seen that the picture shows six men and six ladies: Nos. `1, 3, 5, 7, 9`, and `11` are ladies, and Nos. `2, 4, 6, 8, 10`, and `12` are men. These twelve individuals represent six married couples, all strangers to one another, who, in walking aimlessly about, have got mixed up. But we are only concerned with the man that is wearing a straw hat—Number `10`. The puzzle is to find this man's wife. Examine the six ladies carefully, and see if you can determine which one of them it is.

    I showed the picture at the time to a few friends, and they expressed very different opinions on the matter. One said, "I don't believe he would marry a girl like Number `7`." Another said, "I am sure a nice girl like Number `3` would not marry such a fellow!" Another said, "It must be Number `1`, because she has got as far away as possible from the brute!" It was suggested, again, that it must be Number `11`, because "he seems to be looking towards her;" but a cynic retorted, "For that very reason, if he is really looking at her, I should say that she is not his wife!"

    I now leave the question in the hands of my readers. Which is really Number `10`'s wife?

    The illustration is of necessity considerably reduced from the large scale on which it originally appeared in The Weekly Dispatch (24th May `1903`), but it is hoped that the details will be sufficiently clear to allow the reader to derive entertainment from its examination. In any case the solution given will enable him to follow the points with interest.


     

    Sources:

  • Question

    One day, Harry Potter found a strange notebook in which the following one hundred sentences were written:

    "In this notebook, there is exactly one sentence that is false."

    "In this notebook, there are exactly two sentences that are false."

    "In this notebook, there are exactly three sentences that are false."

    ...

    "In this notebook, there are exactly one hundred sentences that are false."

    Are there any true sentences in this notebook, and if so, how many? Justify your answer!

  • Hans the Brave and the Cruel Law

    In a magical kingdom, there once lived a cruel king. Around his palace was a bridge, and he placed a guard on the bridge who received the following orders: he must ask everyone who crosses the bridge why they have come here. If the person answers falsely, he must be hanged, and if he answers truthfully – he must be beheaded.

    One day, Hans the Brave needed to pass through this place. When the guard asked him: "Why have you come here?", Hans gave such an answer that the guard was forced to release him. What exactly did Hans say to the guard?

  • Hans the Brave and the Cruel Law

    In a magical land, there once lived a cruel king. Near his palace was a bridge, and he placed a guard on the bridge who received the following orders: he must ask everyone who crosses the bridge why they have come there. If the person answers a lie, he must hang him, and if he answers the truth – he must behead him.

    One day, Hans the Brave needed to pass through this place. When the guard asked him: "Why have you come here?", Hans gave such an answer that the guard was forced to release him. What exactly did Hans say to the guard?

  • Question

    All champions eat champion's cereal. Shlomi eats champion's cereal. Does that mean he is a champion?

  • Question

    The company "The Diligent Builder" is engaged in stockpiling trees in a magical forest in Canada. A nature protection association called "The Green Avenger" wants to protect the forest and opposes the company's activity. As a result, the company's CEO said the following sentence:

    "`99%` of the trees in the forest are maple trees. In the coming year, we are going to cut down only maple trees, and as a result, the percentage of maple trees in the forest in a year will become `98%`."

    What percentage of the trees in the forest do the Diligent Builders intend to cut down?

  • Where Did the Extra Thaler Come From?

    A cobbler named Karl made boots and sent his young son Hans to the market to sell them for `25` thalers. When Hans arrived at the market, two disabled men approached him, one without a left leg, the other without a right leg, and asked to buy one boot each. Hans agreed and sold each of them a boot for `12.5` thalers.

    When Hans returned home and told his father what had happened, Karl decided that these people should have been sold boots at a lower price - `10` thalers per boot. So he gave Hans `5` thalers and asked him to return `2.5` thalers to each of them.

    On his way to the market, Hans saw a sweets stall, couldn't resist, and spent `3` thalers of what his father had given him there. After that, he found the two disabled men and gave each of them one thaler, because that's all he had left. When Hans returned home, he regretted what he had done and told his father everything. The cobbler Karl was very angry and locked his son in the pantry as punishment.

    Thus, Hans sits in the pantry and analyzes what happened that day: "I returned one thaler to each of the disabled men, which means that each of them ultimately paid `12.5-1=11.5` thalers for his boot. So in total they paid `11.5*2=23` thalers. And I spent three thalers on sweets. That's a total of  `26` thalers, but there were `25`! Where did one more thaler come from?"