Algebra

Algebra is a broad branch of mathematics that uses symbols (usually letters) to represent numbers and to state rules and relationships. It involves manipulating expressions, solving equations and inequalities, and studying functions and structures. Questions cover a wide range of these topics.

• Question

  Prove that 

  `1+3+5+...+(2n-1)=n^2`

  Topics:

  Combinatorics -> Induction (Mathematical Induction) Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence

• Cherries and Blueberries

  `175` kg of cherries cost more than `125` kg of blueberries, but less than `126` kg of blueberries. In addition, it is known that a kilogram of cherries costs a whole number of shekels, and a kilogram of blueberries also costs a whole number of shekels.

  Prove that `80` shekels is not enough to buy one kilogram of blueberries and three kilograms of cherries.

  S. Fomin

  Topics:

  Number Theory Arithmetic Algebra -> Inequalities Algebra -> Word Problems
  Sources:
  • Tournament of Towns, 1983-1984, Fall, Practice Version, Grades 9-10 Question 1 Points 3

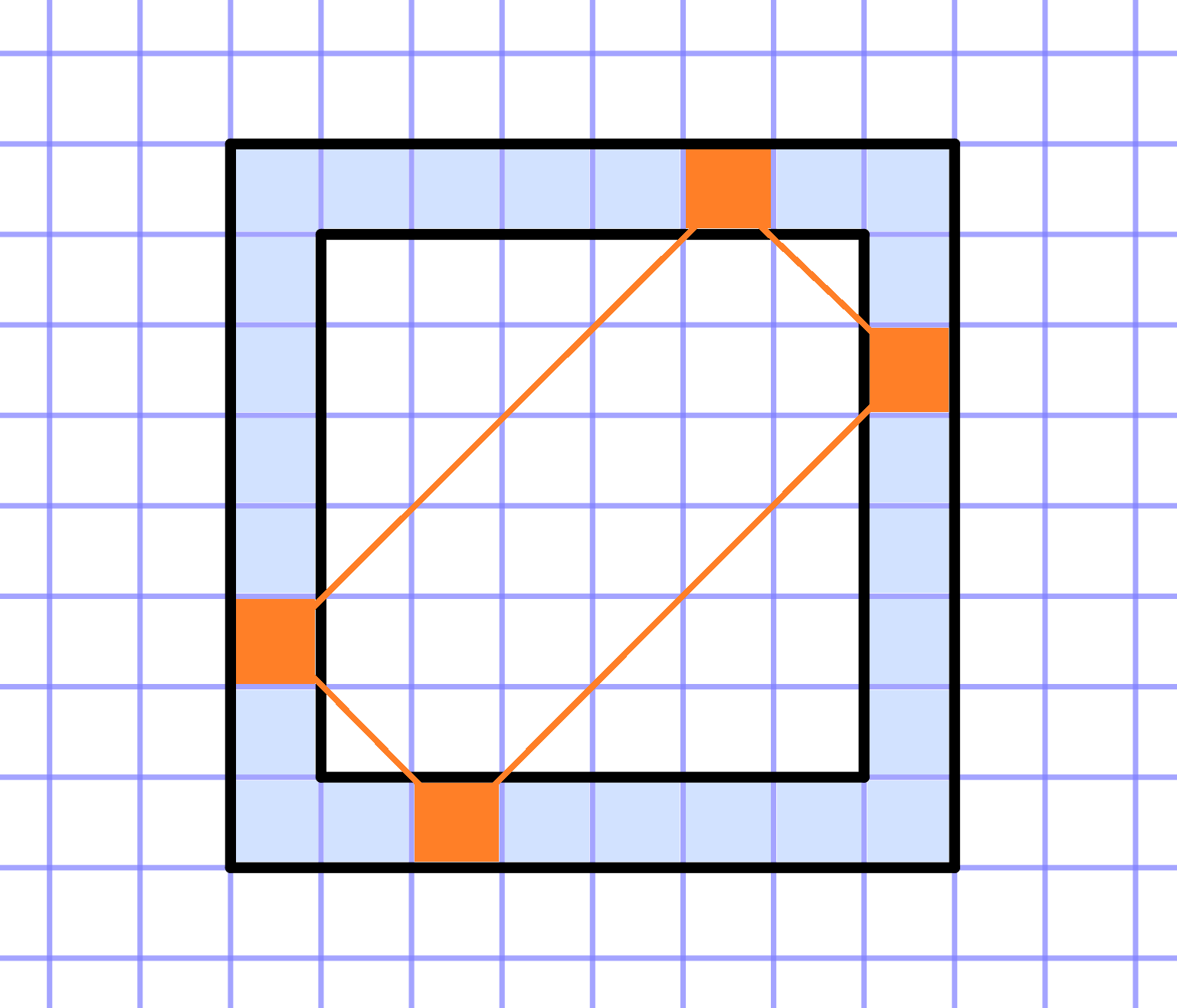
• Frame

  On a grid paper, a square of size `NxxN` is given. Consider its frame with a width of one square. It consists of `4*(N-1)` squares.

  Can you write `4*(N-1)` consecutive integers (not necessarily positive) in the squares of the frame, such that the following condition holds:

  For every rectangle whose vertices are on the frame and whose sides are parallel to the diagonals of the original square, the sum of the numbers at the vertices is equal to a constant value. This also includes the "degenerate" rectangles of zero width that coincide with the diagonals of the square - in this case, simply sum the two numbers at the opposite vertices of the square.

  For:

  a. `N=3`

  b. `N=4`

  c. `N=5`

  

  Topics:

  Arithmetic Number Theory -> Division -> Parity (Even/Odd) Proof and Example -> Constructing an Example / Counterexample Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures
  Sources:
  • Tournament of Towns, 1983-1984, Fall, Practice Version, Grades 9-10 Question 3 Points 2+3+4

• Product of Digits

  For a natural number `x`, let `P(x)` denote the product of the digits of `x`, and let `S(x)` denote the sum of the digits of `x`. 

  How many solutions are there to the equation:

  `P(P(x))+P(S(x))+S(P(x))+S(S(x))=1984`

  Topics:

  Number Theory Algebra -> Equations
  Sources:
  • Tournament of Towns, 1983-1984, Fall, Practice Version, Grades 9-10 Question 4 Points 8

• Question

  Find the value of the expression without a calculator:

  `(sqrt(sqrt(2)-1))/(sqrt(sqrt(2)+1))+ (sqrt(sqrt(3)-sqrt(2)))/(sqrt(sqrt(3)+sqrt(2)))+ (sqrt(2-sqrt(3)))/(sqrt(2+sqrt(3)))`

  Show hint

  Log in here to receive the hint
  Topics:

  Algebra -> Algebraic Techniques -> Short Multiplication Formulas / Algebraic Identities Algebra -> Algebraic Techniques -> Roots / Radicals Algebra -> Algebraic Techniques -> Multiplication by the Conjugate

• Question

  `120` identical spheres are arranged in the shape of a triangular pyramid. How many layers are there in the pyramid?

  Note: This is a pyramid, which is a three-dimensional shape, and not a triangle in a plane.

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Solid Geometry / Geometry in Space Arithmetic Logic -> Reasoning / Logic Proof and Example -> Constructing an Example / Counterexample Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence Algebra -> Sequences -> Complete/Continue the Sequence Number Theory -> Triangular Numbers

• Question

  In a room, there are round chairs with `3` legs and square chairs with `4` legs, totaling `8` chairs. How many of them are square chairs, if the total number of legs in the room is `27`?

  Topics:

  Algebra -> Equations Algebra -> Word Problems

• Question

  In Ella's building, there are three entrances and `13` floors (from `0` to `12`, and the apartments are on every floor except the ground floor). In each entrance, on each floor, there are five apartments. Ella lives in apartment number `73`. In which entrance and on which floor does she live?

  Topics:

  Algebra -> Word Problems Number Theory -> Division Arithmetic -> Division with Remainder

• Question

  Avi invited guests. They know he lives in apartment `333`, in entrance number `10`, but they don't know which floor. There are `9` floors in the building, and it is known that there are an equal number of apartments on each floor. The guests want to use the elevator. Can they calculate in advance which floor they need to press in the elevator?

  Topics:

  Algebra -> Inequalities Algebra -> Word Problems Arithmetic -> Division with Remainder

• Question

  Seven wolves eat seven sheep in seven days. How long will it take `9` wolves to eat `9` sheep?

  Topics:

  Arithmetic Algebra -> Word Problems Logic -> Reasoning / Logic