Algebra

Algebra is a broad branch of mathematics that uses symbols (usually letters) to represent numbers and to state rules and relationships. It involves manipulating expressions, solving equations and inequalities, and studying functions and structures. Questions cover a wide range of these topics.

• Question

  Let the sides of a triangle be a, b, c and the lengths of the corresponding medians be `m_a , m_b, m_c`. Show that

  `sum_{cyc} m_a / a >= {3( m_a + m_b + m_c)} /{a + b + c}`

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Plane Geometry -> Triangles Algebra -> Inequalities Geometry -> Plane Geometry -> Triangle Inequality
  Sources:
  • Mink Exercises and Additional Competition Materials, 2018-2019, Exercise 1

• Question

  For all `a,b,c >=1 ` that satisfy `a+b+c= 2abc `

  Prove that `root (3) ((a+b+c)^2) >= sum_{cyc} root (3) (ab-1) `

  Show hint

  Log in here to receive the hint
  Topics:

  Algebra -> Inequalities -> Averages / Means
  Sources:
  • Mink Exercises and Additional Competition Materials, 2018-2019, Exercise 1

• Signs

  A cyclist is riding on a straight road without turns and sees the following sign by the side of the road:

  

   

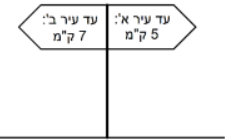
  He continues moving and sees another sign:

  

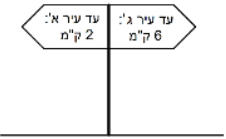
  Find the distance between cities B and C.

  Show hint

  Log in here to receive the hint
  Topics:

  Arithmetic Algebra -> Word Problems
  Sources:
  • Young Mathematician Olympiad, 2017-2018, Stage A, Grades 3-4 Question 1
  • Young Mathematician Olympiad, 2017-2018, Stage A, Grades 5-6 Question 1

• What is the Smiley?

  In the following exercise, one of the digits has been replaced by a smiley face. Find the digit.

  `1☺xx6-☺=70`

  Show hint

  Log in here to receive the hint
  Topics:

  Arithmetic Algebra -> Equations
  Sources:
  • Young Mathematician Olympiad, 2017-2018, Stage A, Grades 3-4 Question 2

• Question

  The numbers a, b, c are different from 0, and the numbers ab, ac, bc are rational.

  a. Show that `a^2+b^2+c^2` is a rational number.

  b. Show that if `a^3+b^3+c^3` is a rational number, then `a+b+c` is a rational number.

  Show hint

  Log in here to receive the hint
  Topics:

  Number Theory Algebra
  Sources:
  • Mink Exercises and Additional Competition Materials, 2018-2019, Exercise 3 Question 1

• 50 to the Power of

  Show that in the rightmost 504 digits of `1+50+50^2+...+50^1000`

  Each digit appears a number of times divisible by 12

  Show hint

  Log in here to receive the hint
  Topics:

  Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules -> Divisibility Rules by 3 and 9 Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence Algebra -> Algebraic Techniques -> Telescoping Sums
  Sources:
  • Mink Exercises and Additional Competition Materials, 2018-2019, Exercise 3 Question 2

• Question

  Given distinct rational numbers a, b, c, prove that `sqrt{1/(a-b)^2+1/(b-c)^2 +1 /(c-a)^2}`

  is rational.

  Show hint

  Log in here to receive the hint
  Topics:

  Number Theory Algebra -> Algebraic Techniques -> Roots / Radicals
  Sources:
  • Mink Exercises and Additional Competition Materials, 2018-2019, Exercise 3 Question 3

• Question

  Given natural numbers m, n such that `m/n <= sqrt 23`, prove that `m/n+3/{mn} <= sqrt 23`

  Show hint

  Log in here to receive the hint
  Topics:

  Number Theory -> Modular Arithmetic / Remainder Arithmetic Algebra -> Inequalities Proof and Example -> Proof by Contradiction Algebra -> Algebraic Techniques -> Roots / Radicals
  Sources:
  • Mink Exercises and Additional Competition Materials, 2018-2019, Exercise 3 Question 4

• Question

  Is there a solution in natural numbers to the equation `x^2 + 12 = y^3` such that

  a. x is even (easier)

  b. x is odd

  Show hint

  Log in here to receive the hint
  Topics:

  Number Theory -> Prime Numbers Number Theory -> Modular Arithmetic / Remainder Arithmetic Number Theory -> Division -> Parity (Even/Odd) Proof and Example -> Proof by Contradiction Arithmetic -> Division with Remainder Algebra -> Equations -> Diophantine Equations
  Sources:
  • Mink Exercises and Additional Competition Materials, 2018-2019, Exercise 3 Question 6

• Question

  Given natural numbers n, a, b such that `3n+1=a^2` and `4n+1=b^2`, prove that:

  a. n is divisible by 8 (easier)

  b. n is divisible by 56

  Show hint

  Log in here to receive the hint
  Topics:

  Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules Algebra -> Equations -> Diophantine Equations
  Sources:
  • Mink Exercises and Additional Competition Materials, 2018-2019, Exercise 3 Question 5