代数学, 数列, 等差数列
等差数列是连续项之间的差是常数(此常数称为公差)的数列。问题涉及寻找第`n`项、前`n`项的和、公差或基于给定信息的其他属性。
-
继续数列
`2, 6, 12, 20, 30…`
a. 数列中的下一个数(第六个数)是什么?
b. 数列中的第`2016`个数是什么?
来源: -
问题
给定一个正整数N,考虑以下过程:记`S(N)`为N的各位数字之和,取`S(N)`的各位数字之和。重复此操作直到得到一个一位数。称执行上述过程直到得到一位数的次数为N的“深度”。例如,49的深度为`S(49)=13 -> S(13)=4)2`,执行了两次操作(49的深度为2),而45的深度为1。
a) 证明对于任何数N,其深度都是有限的,也就是说,在过程的某个阶段总会得到一个一位数。
b) 记`x(n)`为深度为N的最小数(值最小的数)。求`x(5776)`除以6的余数。请说明你的答案!
c) 求`x(5776) - x(5708)`除以2016的余数。请说明你的答案!
来源: -
问题
求从`1`到`100`的所有自然数之和。
-
问题
黑板上写着数字:`1, 2, 3, …, 2016, 2017`。每次操作可以选择黑板上的两个数字,将它们擦除,然后写上它们的(正)差。经过多次这样的操作后,黑板上只剩下一个数字。这可能为零吗?
-
问题
是否存在仅由素数组成的无穷等差数列?
注意:我们不考虑“平凡”的等差数列,即常数列。
-
问题
所有不超过 `100` 的偶数之和比所有不超过 `100` 的奇数之和大多少?
-
问题
证明以下等式:
`1+3+5+...+(2n-1)=n^2`
-
框架
在一个给定的方格纸上有一个大小为 `NxxN` 的正方形。我们考虑其厚度为一个方格的框架。它由 `4*(N-1)` 个方格组成。
你是否能将 `4*(N-1)` 个连续整数(不一定是正数)填入框架的方格中,使得满足以下条件:
对于每个顶点都在框架上且边与原始正方形的对角线平行的矩形,其顶点上的数字之和等于一个常数。 这也包括“退化”的宽度为零的矩形,这些矩形与正方形的对角线重合 - 在这种情况下,只需将正方形的相对顶点的两个数字相加
对于:
a. `N=3`
b. `N=4`
c. `N=5`
来源: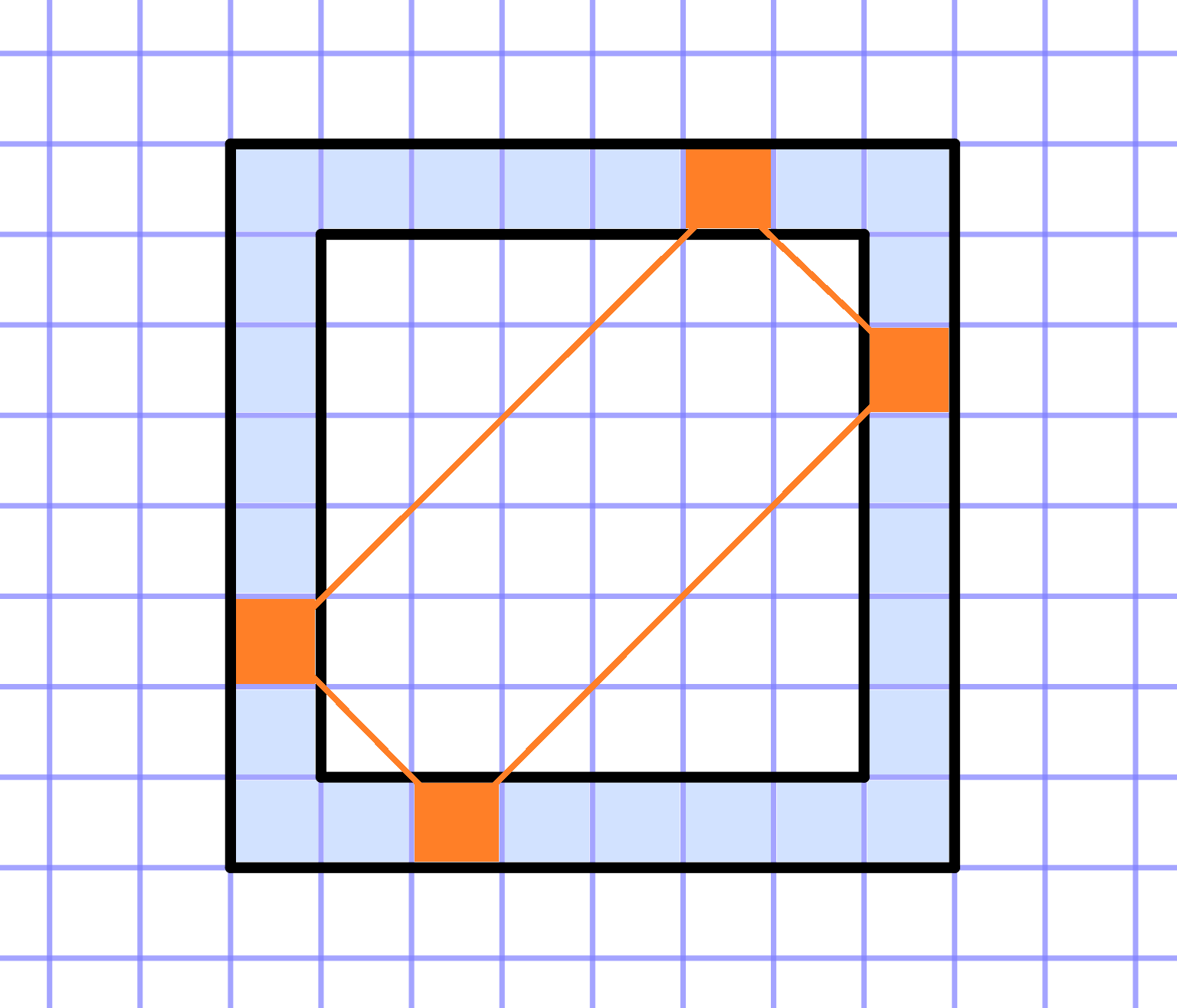
-
问题
`120` 个相同的球被排列成一个三角形金字塔。金字塔有多少层?
注意:这是一个金字塔,即三维形状,而不是平面上的三角形。
-
问题
给定序列 `1 , 1/2 ,1/3 ,1/4 ,1/5,...`,是否存在一个由上述序列的项组成的等差数列?
-
长度为 5
-
任意长度
来源: -