集合论
集合论是关于集合(对象集合)的基础数学理论。它处理集合运算(并集、交集、补集、差集)、集合属性(基数、子集)和集合之间的关系。问题涉及维恩图、集合表示法和属性。
-
问题
圆周上给定一些蓝色和红色的点。允许添加一个红点并改变其相邻点的颜色,或者移除一个红点并改变其先前相邻点的颜色(不允许在圆周上留下少于 2 个点)。证明仅通过这些操作不可能将具有两个红点的圆周转换为具有两个蓝点的圆周。
来源:
K. Kazarnovski -
问题
一群孩子去了一个游乐园。已知戴帽子的女孩的数量等于没戴帽子的男孩的数量。
在这个群体中,没戴帽子的孩子多还是女孩多?
来源: -
米奇
有很多猫叫米奇。 那么哪个更多:除了不叫米奇的猫之外的猫,还是叫米奇的名字的动物,除了那些不是猫的动物?
来源: -
森林中的松树
护林员正在数森林中的松树。他沿着图中每个圆圈走了一圈,并且在每个圆圈内他数了正好 `3` 棵松树。证明护林员肯定数错了。

-
圆圈
六年级有 `70` 个学生。其中 `27` 人参加戏剧社,`32` 人在合唱团唱歌,`22` 人练习柔道。戏剧社有 `10` 个合唱团成员,合唱团有 `6` 个柔道成员,柔道社有 `8` 个也参加戏剧社的成员。有三个孩子同时参加戏剧社、柔道社和合唱团。那么有多少六年级的学生没有参加这三个社团中的任何一个?
-
问题
гимназии的每个学生至少懂以下两种古代语言中的一种:拉丁语或古希腊语。已知 `85%` 的学生懂拉丁语,`75%` 的学生懂希腊语。那么,懂这两种语言的学生占百分之多少?
-
问题
汉娜在等公共汽车。以下三个事件中,哪个事件发生的概率最大?
- 汉娜等公共汽车至少一分钟,
- 汉娜等公共汽车至少两分钟,
- 汉娜等公共汽车至少五分钟。
-
问题
在`1`到`100`之间有多少个数既不能被`2`整除,也不能被`5`整除?
主题:算术 数论 -> 模算术/余数算术 -> 整除规则 -> 被2、4和8整除的规则 数论 -> 模算术/余数算术 -> 整除规则 -> 被5和25整除的规则 数论 -> 最大公约数(GCD)和最小公倍数(LCM) 集合论 数论 -> 除法 -
花盆浇水
汉娜和瑞秋在家里给花盆浇水。已知她们每人浇了家里一半数量的花盆,也知道有三个花盆被错误地浇了两次。还有多少花盆需要浇水?
-
问题
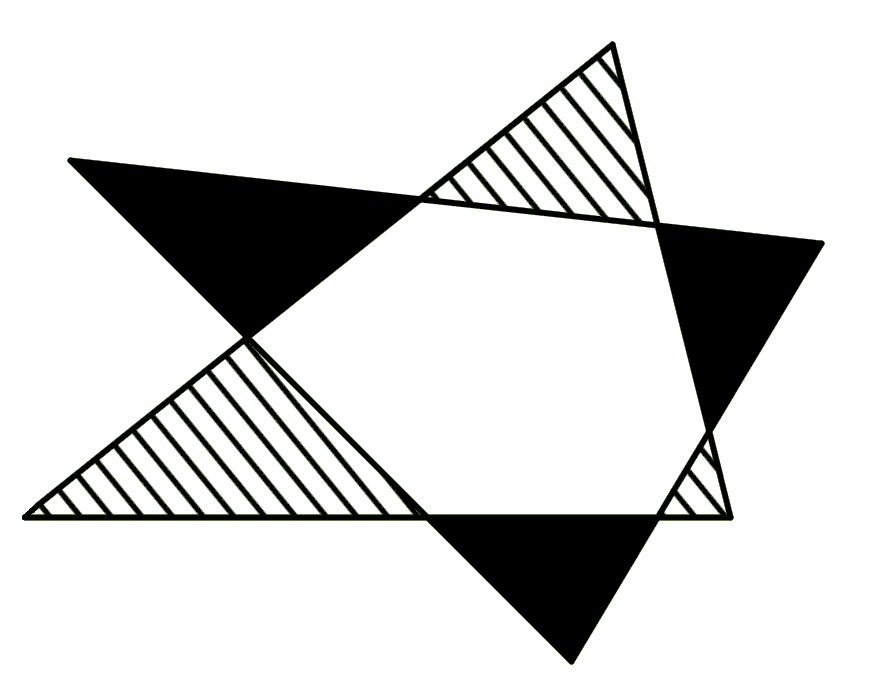
两个全等的三角形形成一个如图像所示的六芒星。证明阴影区域的面积等于条纹区域的面积。