Geometry, Solid Geometry / Geometry in Space, Polyhedra

Polyhedra are three-dimensional geometric solids whose faces are polygons. This topic covers their properties, such as the number of faces, edges, and vertices, and relationships like Euler's formula (`V-E+F=2`). Questions might involve identifying types of polyhedra and analyzing their structures.

• Question

  Suppose two pyramids are tangent to each other if they have no common interior points and they intersect in a non-degenerate planar polygon. Is it possible for 8 pyramids in space to all be tangent to each other? 
  A. Angeles 

  Topics:

  Combinatorics -> Combinatorial Geometry Proof and Example -> Constructing an Example / Counterexample Geometry -> Solid Geometry / Geometry in Space -> Polyhedra
  Sources:
  • Tournament of Towns, 1980-1981, Spring, Main Version, Grades 11-12 Question 1 Points 7

• Question

  Prove that there is no polyhedron with `7` edges.

  Topics:

  Combinatorics -> Graph Theory Proof and Example -> Proof by Contradiction Geometry -> Solid Geometry / Geometry in Space -> Polyhedra

• Question

  Prove that every polyhedron has at least two faces with the same number of edges.

  Topics:

  Combinatorics -> Pigeonhole Principle Combinatorics -> Graph Theory Geometry -> Solid Geometry / Geometry in Space -> Polyhedra

• Question

  A square is divided into several convex polygons (more than `1`), each of which has a different number of sides. Prove that among these polygons there is a triangle.

  Topics:

  Combinatorics -> Pigeonhole Principle Combinatorics -> Combinatorial Geometry Combinatorics -> Graph Theory Geometry -> Plane Geometry -> Triangles Proof and Example -> Proof by Contradiction Geometry -> Solid Geometry / Geometry in Space -> Polyhedra Minimum and Maximum Problems / Optimization Problems

• BUILDING THE TETRAHEDRON

  I possess a tetrahedron, or triangular pyramid, formed of six sticks glued together, as shown in the illustration. Can you count correctly the number of different ways in which these six sticks might have been stuck together so as to form the pyramid?

  Some friends worked at it together one evening, each person providing himself with six lucifer matches to aid his thoughts; but it was found that no two results were the same. You see, if we remove one of the sticks and turn it round the other way, that will be a different pyramid. If we make two of the sticks change places the result will again be different. But remember that every pyramid may be made to stand on either of its four sides without being a different one. How many ways are there altogether?

  

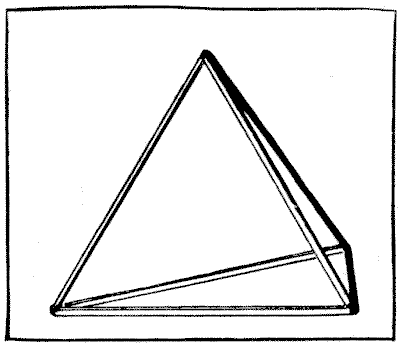  Topics:

  Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Geometry -> Solid Geometry / Geometry in Space -> Polyhedra
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 280

• PAINTING A PYRAMID

  This puzzle concerns the painting of the four sides of a tetrahedron, or triangular pyramid. If you cut out a piece of cardboard of the triangular shape shown in Fig. `1`, and then cut half through along the dotted lines, it will fold up and form a perfect triangular pyramid. And I would first remind my readers that the primary colours of the solar spectrum are seven—violet, indigo, blue, green, yellow, orange, and red. When I was a child I was taught to remember these by the ungainly word formed by the initials of the colours, "Vibgyor."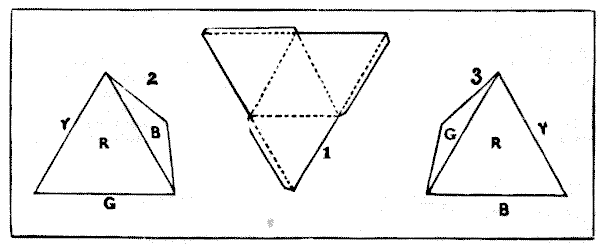 In how many different ways may the triangular pyramid be coloured, using in every case one, two, three, or four colours of the solar spectrum? Of course a side can only receive a single colour, and no side can be left uncoloured. But there is one point that I must make quite clear. The four sides are not to be regarded as individually distinct. That is to say, if you paint your pyramid as shown in Fig. `2` (where the bottom side is green and the other side that is out of view is yellow), and then paint another in the order shown in Fig. `3`, these are really both the same and count as one way. For if you tilt over No. `2` to the right it will so fall as to represent No. `3`. The avoidance of repetitions of this kind is the real puzzle of the thing. If a coloured pyramid cannot be placed so that it exactly resembles in its colours and their relative order another pyramid, then they are different. Remember that one way would be to colour all the four sides red, another to colour two sides green, and the remaining sides yellow and blue; and so on.
  Topics:

  Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Geometry -> Solid Geometry / Geometry in Space -> Polyhedra
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 281

• Question

  A regular polygon with 4k sides is divided into parallelograms. Prove that among these parallelograms there are at least k rectangles. Find the sum of the areas of all the rectangles.

  Topics:

  Geometry -> Plane Geometry Geometry -> Area Calculation Geometry -> Solid Geometry / Geometry in Space -> Polyhedra -> Regular Polyhedra

• THE PENTAGON AND SQUARE

  I wonder how many of my readers, amongst those who have not given any close attention to the elements of geometry, could draw a regular pentagon, or five-sided figure, if they suddenly required to do so. A regular hexagon, or six-sided figure, is easy enough, for everybody knows that all you have to do is to describe a circle and then, taking the radius as the length of one of the sides, mark off the six points round the circumference. But a pentagon is quite another matter. So, as my puzzle has to do with the cutting up of a regular pentagon, it will perhaps be well if I first show my less experienced readers how this figure is to be correctly drawn. Describe a circle and draw the two lines H B and D G, in the diagram, through the centre at right angles. Now find the point A, midway between C and B. Next place the point of your compasses at A and with the distance A D describe the arc cutting H B at E. Then place the point of your compasses at D and with the distance D E describe the arc cutting the circumference at F. Now, D F is one of the sides of your pentagon, and you have simply to mark off the other sides round the circle. Quite simple when you know how, but otherwise somewhat of a poser.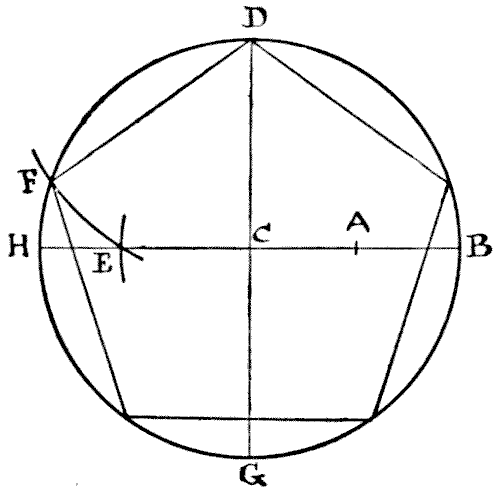 Having formed your pentagon, the puzzle is to cut it into the fewest possible pieces that will fit together and form a perfect square.
  Topics:

  Geometry -> Plane Geometry Geometry -> Area Calculation Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Geometry -> Solid Geometry / Geometry in Space -> Polyhedra -> Regular Polyhedra
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 155

• THE FLY ON THE OCTAHEDRON

  "Look here," said the professor to his colleague, "I have been watching that fly on the octahedron, and it confines its walks entirely to the edges. What can be its reason for avoiding the sides?"

  "Perhaps it is trying to solve some route problem," suggested the other. "Supposing it to start from the top point, how many different routes are there by which it may walk over all the edges, without ever going twice along the same edge in any route?"

   

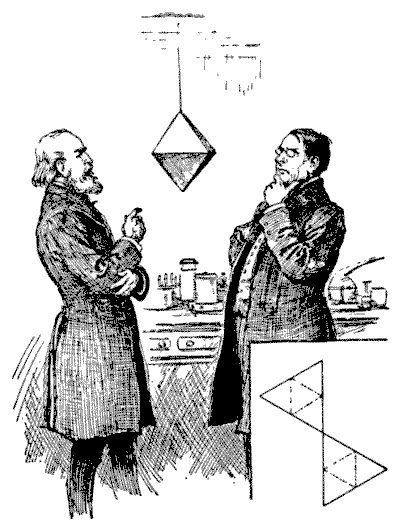
  The problem was a harder one than they expected, and after working at it during leisure moments for several days their results did not agree—in fact, they were both wrong. If the reader is surprised at their failure, let him attempt the little puzzle himself. I will just explain that the octahedron is one of the five regular, or Platonic, bodies, and is contained under eight equal and equilateral triangles. If you cut out the two pieces of cardboard of the shape shown in the margin of the illustration, cut half through along the dotted lines and then bend them and put them together, you will have a perfect octahedron. In any route over all the edges it will be found that the fly must end at the point of departure at the top.

  Topics:

  Combinatorics -> Combinatorial Geometry Combinatorics -> Graph Theory Geometry -> Solid Geometry / Geometry in Space -> Polyhedra -> Regular Polyhedra
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 245

• THE ICOSAHEDRON PUZZLE

  The icosahedron is another of the five regular, or Platonic, bodies having all their sides, angles, and planes similar and equal. It is bounded by twenty similar equilateral triangles. If you cut out a piece of cardboard of the form shown in the smaller diagram, and cut half through along the dotted lines, it will fold up and form a perfect icosahedron.

  Now, a Platonic body does not mean a heavenly body; but it will suit the purpose of our puzzle if we suppose there to be a habitable planet of this shape. We will also suppose that, owing to a superfluity of water, the only dry land is along the edges, and that the inhabitants have no knowledge of navigation. If every one of those edges is `10,000` miles long and a solitary traveller is placed at the North Pole (the highest point shown), how far will he have to travel before he will have visited every habitable part of the planet—that is, have traversed every one of the edges?

  

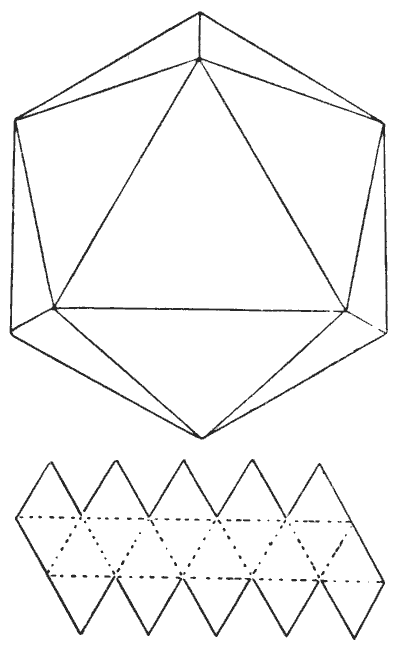  Topics:

  Combinatorics -> Combinatorial Geometry Combinatorics -> Graph Theory Geometry -> Solid Geometry / Geometry in Space -> Polyhedra -> Regular Polyhedra
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 246