גאומטריה, גאומטריה במרחב, פאונים

פאונים הם גופים גאומטריים תלת-ממדיים שפאותיהם הן מצולעים. נושא זה מכסה את תכונותיהם, כגון מספר הפאות, המקצועות והקדקודים, ויחסים כמו נוסחת אוילר (`V-E+F=2`). שאלות עשויות לכלול זיהוי סוגי פאונים וניתוח מבניהם.

• שאלה

  נגיד ששתי פירמידות משיקות זו לזו אם אין להן נקודות פנימיות משותפות והן נחתכות במצולע מישורי לא מנוון. האם ייתכן ש 8 פירמידות במרחב ישיקו כולם אחת לשנייה? 
  א. אנג'אנס 

  נושאים:

  קומבינטוריקה -> גאומטריה קומבינטורית הוכחה ודוגמה -> בניית דוגמה גאומטריה -> גאומטריה במרחב -> פאונים
  מקורות:
  • תחרות הערים, תשמ"א, אביב, גרסה עיקרית, כיתות י"א-י"ב שאלה 1 נקודות 7

• שאלה

  הוכיחו כי לא קיים פאון בעל `7` מקצועות.

  נושאים:

  קומבינטוריקה -> תורת הגרפים הוכחה ודוגמה -> הוכחה בשלילה גאומטריה -> גאומטריה במרחב -> פאונים

• שאלה

  הוכיחו שלכל פאון יש שתי פאות עם כמות זהה של מקצועות.

  נושאים:

  קומבינטוריקה -> עקרון שובך היונים קומבינטוריקה -> תורת הגרפים גאומטריה -> גאומטריה במרחב -> פאונים

• שאלה

  ריבוע מחולק לכמה מצולעים קמורים (יותר מ-`1`), שלכל אחד מהם יש מספר שונה של צלעות. הוכיחו כי בין המצולעים האלה יש משולש.

  נושאים:

  קומבינטוריקה -> עקרון שובך היונים קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת הגרפים גאומטריה -> גאומטריה במישור -> משולשים הוכחה ודוגמה -> הוכחה בשלילה גאומטריה -> גאומטריה במרחב -> פאונים בעיות מינימום ומקסימום

• בניית הטטרהדרון

  יש לי טטרהדרון, או פירמידה משולשת, העשויה משישה מקלות המודבקים זה לזה, כפי שמוצג באיור. האם תוכלו לספור נכונה את מספר הדרכים השונות שבהן ניתן היה להדביק את ששת המקלות הללו יחד כדי ליצור את הפירמידה?

  כמה חברים עבדו על זה יחד בערב אחד, כאשר כל אדם מצטייד בשישה גפרורים כדי לעזור למחשבותיו; אבל התברר שאף שתי תוצאות לא היו זהות. אתם רואים, אם נסיר אחד מהמקלות ונסובב אותו לצד השני, זו תהיה פירמידה שונה. אם נחליף בין שניים מהמקלות התוצאה שוב תהיה שונה. אבל זכרו שניתן להעמיד כל פירמידה על כל אחד מארבעת צדדיה מבלי להיות פירמידה שונה. כמה דרכים יש בסך הכל?

  

  נושאים:

  קומבינטוריקה -> בדיקת מקרים -> תהליכים גאומטריה -> גאומטריה במרחב -> פאונים
  מקורות: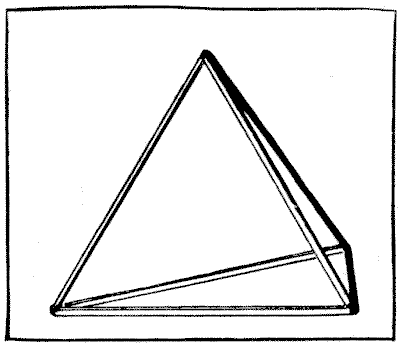
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 280

• צביעת פירמידה

  חידה זו עוסקת בצביעת ארבעת צדדיו של טטרהדרון, או פירמידה משולשת. אם תגזרו חתיכת קרטון בצורה משולשת כפי שמוצג באיור `1`, ואז תחצו אותה לאורך הקווים המקווקווים, היא תתקפל ותצור פירמידה משולשת מושלמת. ברצוני להזכיר לקוראיי שצבעי היסוד של הספקטרום הסולארי הם שבעה - סגול, אינדיגו, כחול, ירוק, צהוב, כתום ואדום. כשהייתי ילד לימדו אותי לזכור אותם באמצעות המילה המגושמת שנוצרה על ידי ראשי התיבות של הצבעים, "Vibgyor".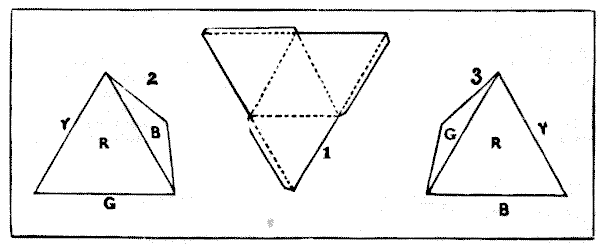 בכמה דרכים שונות ניתן לצבוע את הפירמידה המשולשת, תוך שימוש בכל מקרה בצבע אחד, שניים, שלושה או ארבעה מצבעי הספקטרום הסולארי? כמובן שצד יכול לקבל רק צבע בודד, ואף צד לא יכול להישאר לא צבוע. אבל יש נקודה אחת שאני חייב להבהיר. אין לראות בארבעת הצדדים כנפרדים מבחינה אינדיבידואלית. כלומר, אם תצבעו את הפירמידה שלכם כפי שמוצג באיור `2` (כאשר הצד התחתון ירוק והצד השני שאינו נראה הוא צהוב), ואז תצבעו אחרת בסדר המוצג באיור `3`, אלה באמת אותו הדבר ונספרים כדרך אחת. כי אם תטו את מס' `2` ימינה, הוא ייפול כך שייצג את מס' `3`. הימנעות מחזרות מסוג זה היא החידה האמיתית של העניין. אם לא ניתן למקם פירמידה צבעונית כך שתדמה בדיוק בצבעיה ובסדר היחסי שלהם לפירמידה אחרת, אז הן שונות. זכרו שדרך אחת תהיה לצבוע את כל ארבעת הצדדים באדום, אחרת לצבוע שני צדדים בירוק, ואת הצדדים הנותרים בצהוב וכחול; וכן הלאה.
  נושאים:

  קומבינטוריקה -> בדיקת מקרים -> תהליכים גאומטריה -> גאומטריה במרחב -> פאונים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 281

• שאלה

  מצולע משוכלל בעל 4k צלעות מחולק למקביליות. הוכיחו שבין המקביליות האלו יש לפחות k מלבנים. מצאו את סכום שטחי כל המלבנים.

  נושאים:

  גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במרחב -> פאונים -> פאונים משוכללים

• שאלה

  נתון מצולע משוכלל. על כל צלע בונים משולש ישר זווית ושווה-שוקיים, כך שהצלע היא היתר של המשולש, וקודקוד הראש בפנים המצולע. מחברים את קודקודי הראש של כל המשולשים ומקבלים מצולע (משוכלל, בעל אותו מספר צלעות). כמה צלעות יש למצולע המקורי, אם שטחו של המצולע שהתקבל הוא חצי משטח המצולע המקורי?

  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> חשבון זוויות גאומטריה -> גאומטריה במרחב -> פאונים -> פאונים משוכללים
  מקורות:
  • מבחני בחירה ל-IMO בישראל, תשע"א, שלב א שאלה 7

• שאלה

  נתון מצולע משוכלל. על כל צלע של המצולע בונים משולש שווה-צלעות מחוץ למצולע.
  כשמחברים את הקודקודים החדשים של כל המשולשים בזה אחר זה, מקבלים מצולע
  משוכלל חדש בעל אותו מספר צלעות כמו המצולע המקורי. כמה צלעות יש למצולע המקורי
  אם שטחו של המצולע החדש גדול פי שלושה משטח המצולע המקורי?
  נושאים:

  גאומטריה -> טריגונומטריה גאומטריה -> חשבון שטחים אלגברה -> משוואות גאומטריה -> גאומטריה במישור -> חשבון זוויות גאומטריה -> גאומטריה במרחב -> פאונים -> פאונים משוכללים
  מקורות:
  • מבחני בחירה ל-IMO בישראל, תשע"ב, שלב א שאלה 7

• המחומש והריבוע

  מעניין אותי כמה מקוראיי, מבין אלה שלא הקדישו תשומת לב רבה ליסודות הגיאומטריה, יוכלו לצייר מחומש משוכלל, או צורה בעלת חמש צלעות, אם יידרשו לעשות זאת באופן פתאומי. משושה משוכלל, או צורה בעלת שש צלעות, הוא די קל, כי כולם יודעים שכל מה שצריך לעשות הוא לתאר מעגל ואז, לקחת את הרדיוס כאורך אחת הצלעות, ולסמן את שש הנקודות סביב ההיקף. אבל מחומש הוא עניין אחר לגמרי. אז, מכיוון שהחידה שלי קשורה לחיתוך של מחומש משוכלל, אולי כדאי שאקודם כל אראה לקוראים הפחות מנוסים שלי איך יש לצייר צורה זו בצורה נכונה. תארו מעגל וציירו את שני הקווים H B ו-D G, בתרשים, דרך המרכז בזוויות ישרות. כעת מצאו את הנקודה A, באמצע בין C ו-B. לאחר מכן הניחו את חוד המצפן שלכם ב-A ועם המרחק A D תארו את הקשת החותכת את H B ב-E. לאחר מכן הניחו את חוד המצפן שלכם ב-D ועם המרחק D E תארו את הקשת החותכת את ההיקף ב-F. כעת, D F היא אחת הצלעות של המחומש שלכם, ועליכם פשוט לסמן את הצלעות האחרות סביב המעגל. די פשוט כשאתם יודעים איך, אבל אחרת קצת קשה.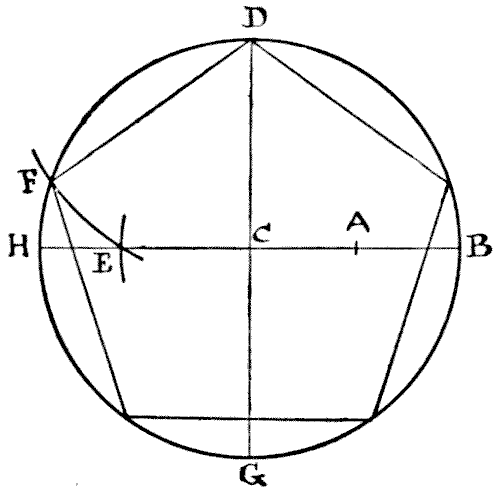 לאחר שיצרתם את המחומש שלכם, החידה היא לחתוך אותו למספר המועט ביותר של חלקים שיתאימו זה לזה וייצרו ריבוע מושלם.
  נושאים:

  גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה גאומטריה -> גאומטריה במרחב -> פאונים -> פאונים משוכללים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 155