组合数学, 着色问题, 棋盘着色
棋盘着色使用标准棋盘(或类似的网格着色)的交替黑白模式作为解决问题的工具,特别是涉及在网格上铺砖、覆盖或移动的问题。它是不变量或奇偶性论证的具体应用。
-
问题
圆周上给定一些蓝色和红色的点。允许添加一个红点并改变其相邻点的颜色,或者移除一个红点并改变其先前相邻点的颜色(不允许在圆周上留下少于 2 个点)。证明仅通过这些操作不可能将具有两个红点的圆周转换为具有两个蓝点的圆周。
来源:
K. Kazarnovski -
问题
是否可以用多米诺骨牌铺满一个`5xx5`的棋盘?
注意:棋盘的每个方格大小与多米诺骨牌的方格大小相同。
-
问题
一个国际象棋的马从 `a1` 格出发,经过若干步后回到了同一格。
马有可能走了奇数步吗?
-
问题
一个骑士从 `a1` 格出发,到达 `h8` 格。是否可能它在途中恰好访问了棋盘上的每个格子一次?
-
问题
从棋盘上切掉两个对角(例如,`a1` 和 `h8`)。 你能用多米诺骨牌铺满剩下的棋盘吗?
-
问题
证明不能将给定的形状切割成多米诺骨牌:

-
问题
你能否将左侧的形状切割成六个与右侧形状相同的形状?
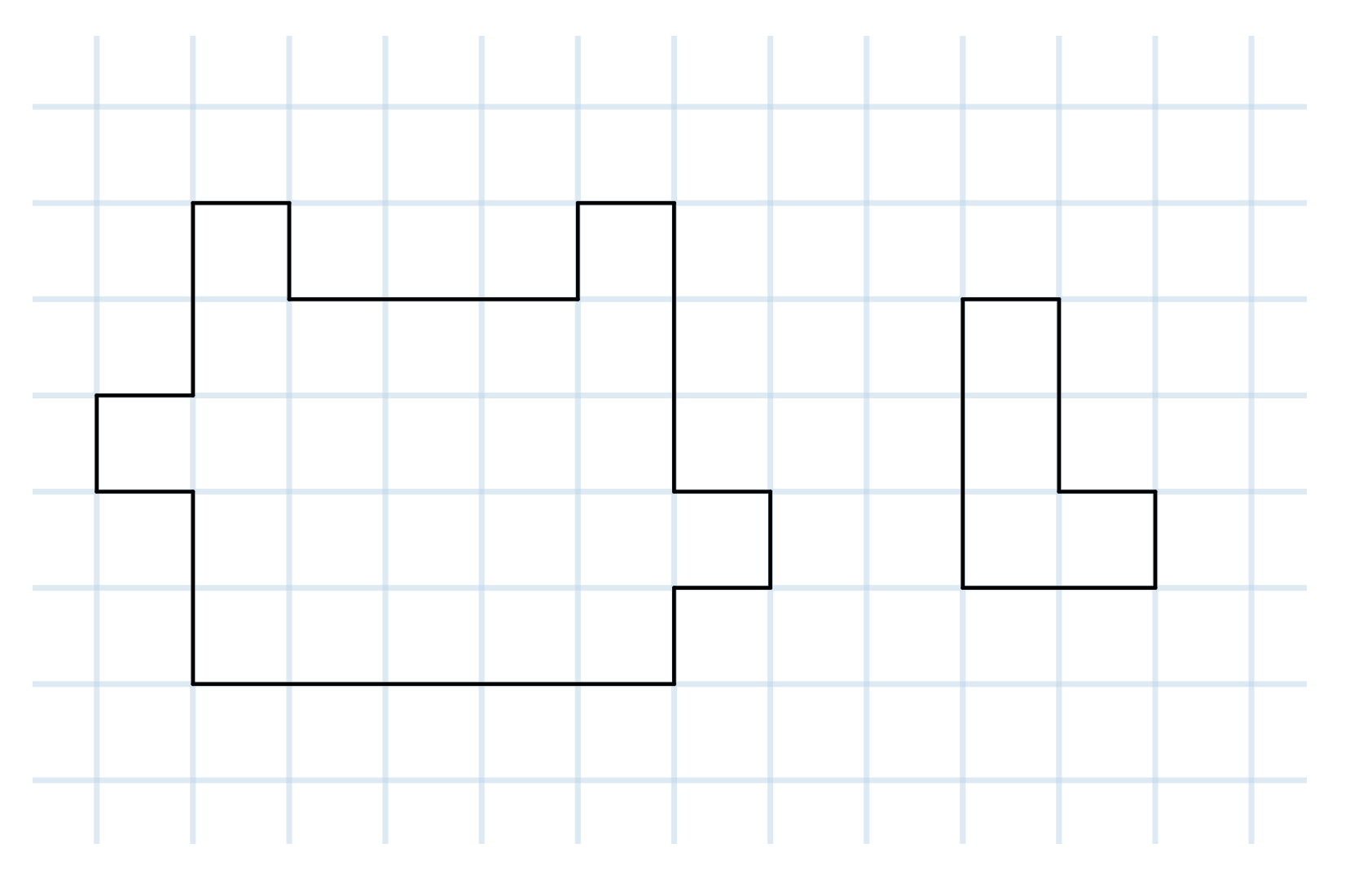
-
问题
Shlomi 有一个棋盘和一个立方体,其面的大小与棋盘上一个正方形的大小相同。 Shlomi 想要将立方体的面涂成黑色和白色,然后将立方体在棋盘上滚动,使得每次接触棋盘的面与它接触的正方形颜色相同。立方体应该恰好一次通过棋盘上的每个正方形。 Shlomi 能做到吗?解释或给出一个例子。
-
乘法表中的差
将`10xx10`的乘法表用黑白棋盘格着色,使得`1xx1`的格子是黑色的。
求所有黑色格子中的数字之和与所有白色格子中的数字之和的差。
1 2 3 4 5 6 7 8 9 10 1 1 2 3 4 5 6 7 8 9 10 2 2 4 6 8 10 12 14 16 18 20 3 3 6 9 12 15 18 21 24 27 30 4 4 8 12 16 20 24 28 32 36 40 5 5 10 15 20 25 30 35 40 45 50 6 6 12 18 24 30 36 42 48 54 60 7 7 14 21 28 35 42 49 56 63 70 8 8 16 24 32 40 48 56 64 72 80 9 9 18 27 36 45 54 63 72 81 90 10 10 20 30 40 50 60 70 80 90 100 来源: -
蚱蜢
有一张无限大的方格纸,一只蚱蜢位于其中的一个方格中。 蚱蜢可以沿水平或垂直方向跳跃两个方格,并且它可以沿对角线跳跃到相邻的方格。 蚱蜢是否能到达与起始方格相邻的方格?
来源: