גאומטריה, גאומטריה במישור, משולשים, דמיון משולשים

דמיון משולשים עוסק במשולשים בעלי אותה צורה אך ייתכן שבגדלים שונים. משמעות הדבר היא שהזוויות המתאימות שלהם שוות והצלעות המתאימות פרופורציונליות. שאלות כוללות הוכחת דמיון (באמצעות משפטי דמיון ז.ז, צ.צ.צ, צ.ז.צ) ושימוש בפרופורציות אלו למציאת אורכים לא ידועים.

• שאלה

  נתון חרוט (בעל ציר סימטריה במרכזו, המאונך לבסיסו) שגובהו 6 ובסיסו הוא עיגול בעל רדיוס `sqrt2` . בתוך החרוט חסומה קובייה – היא מונחת על בסיס החרוט וכל קדקודיה העליונים נוגעים בחרוט. מצאו את אורך הצלע של הקובייה. נמקו את תשובתכם.

  

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
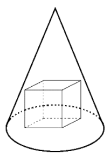  נושאים:

  גאומטריה -> גאומטריה במרחב אלגברה -> משוואות גאומטריה -> גאומטריה במישור -> משפט פיתגורס גאומטריה -> גאומטריה במישור -> משולשים -> דמיון משולשים
  מקורות:
  • אולימפיאדת גיליס, תשע"ו שאלה 2

• שאלה

  משולש שרירותי מעבירים משיקים למעגל החסום, במקביל לצלעות המשולש. המשיקים האלה חותכים מהמשולש המקורי שלושה משולשים קטנים. הוכיחו כי סכום הרדיוסים של המעגלים החסומים במשולשים האלה שווה לרדיוס המעגל החסום במשולש המקורי.

  נושאים:

  גאומטריה -> גאומטריה במישור -> מעגלים -> משיק למעגל גאומטריה -> גאומטריה במישור -> משולשים -> דמיון משולשים