גאומטריה, גאומטריה במישור, משפט פיתגורס

משפט פיתגורס הוא קשר יסודי בגאומטריה אוקלידית בין שלוש צלעותיו של משולש ישר-זווית. הוא קובע שריבוע היתר (הצלע שמול הזווית הישרה) שווה לסכום ריבועי שתי הצלעות האחרות (`a^2 + b^2 = c^2`). שאלות כוללות יישום משפט זה למציאת אורכי צלעות.

  • ריבוע הפורניר

    הבא מייצג חתיכת עץ ברשותי, `5` אינץ' מרובע. על ידי סימונים על פני השטח הוא מחולק לעשרים וחמישה אינצ'ים מרובעים. אני רוצה לגלות דרך לחתוך את חתיכת העץ הזו למספר המינימלי האפשרי של חלקים שיתאימו יחד וייצרו שני ריבועים מושלמים בגדלים שונים ובמידות ידועות. אבל, לצערי, בכל אחד משש עשרה הצמתים של קווי החיתוך נתקע מסמר קטן מתישהו, והמסור הנימי שלי ייפגע אם הוא יבוא במגע עם אחד מאלה. לכן אני צריך למצוא שיטה לעשות את העבודה שלא תחייב אותי לחתוך דרך אף אחת משש עשרה הנקודות האלה. איך זה אמור להיעשות? זכור, יש לתת את המידות המדויקות של שני הריבועים. מקורות:

  • חיתוך לינולאום

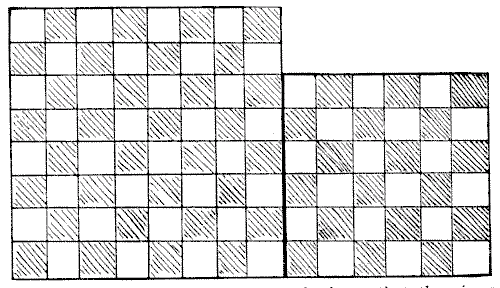    הדיאגרמה כאן מייצגת שני חלקי לינולאום נפרדים. דוגמת המשבצות לא חוזרת על עצמה בגב, כך שלא ניתן להפוך את החלקים. החידה היא לחתוך את שתי הריבועים לארבעה חלקים כך שהם יתאימו זה לזה וייצרו ריבוע מושלם אחד בגודל `10`×`10`, כך שהדוגמה תתאים כראוי, וכך שלחלק הגדול יותר יהיה חלק קטן ככל האפשר שנחתך ממנו. מקורות:

  • גְּנֵבַת חַבְלֵי הַפַּעֲמוֹנִים

    שְׁנֵי אֲנָשִׁים פָּרְצוּ לְמִגְדַּל כְּנֵסִיָּה לַיְלָה אֶחָד כְּדֵי לִגְנֹב אֶת חַבְלֵי הַפַּעֲמוֹנִים. שְׁנֵי הַחֲבָלִים עָבְרוּ דֶּרֶךְ חֹרִים בַּתִּקְרָה הָעֲשׂוּיָה עֵץ שֶׁהָיְתָה מֵעֲלֵיהֶם, וְהֵם לֹא בִּזְבְּזוּ זְמַן וְטִפְּסוּ לְרֹאשׁ הַמִּגְדָּל. אָז אִישׁ אֶחָד שָׁלַף אֶת סַכִּינוֹ וְחָתַךְ אֶת הַחֶבֶל מֵעַל רֹאשׁוֹ, וּכְתוֹצָה מִכָּךְ הוּא נָפַל עַל הָרִצְפָּה וְנִפְצַע קָשׁוֹת. חֲבֵרוֹ-הַגַּנָּב קָרָא שֶׁמַּגִּיעַ לוֹ עַל שֶׁהוּא כָּזֶה טִפֵּשׁ. הוּא אָמַר שֶׁהוּא הָיָה צָרִיךְ לַעֲשׂוֹת כְּפִי שֶׁהוּא עוֹשֶׂה, וְעַל כֵּן הוּא חָתַךְ אֶת הַחֶבֶל מִתַּחַת לַמָּקוֹם שֶׁבּוֹ הוּא הֶחְזִיק. אָז, לְתַדְהֵמָתוֹ, הוּא גִּלָּה שֶׁהוּא לֹא בְּמַצָּב טוֹב יוֹתֵר, כִּי אַחֲרֵי שֶׁנִּתְלָה כָּל עוֹד כֹּחוֹ הֶחְזִיק מַעֲמָד, הוּא הֻכְרַח לְהַרְפּוֹת וְלִנְפֹּל לְצַד חֲבֵרוֹ. כָּאן שְׁנֵיהֶם נִמְצְאוּ לְמָחֳרָת בַּבֹּקֶר עִם גְּפָפִים שְׁבוּרִים. מָה הָיָה גֹּבַהּ הַנְּפִילָה שֶׁלָּהֶם? אֶחָד מֵהַחֲבָלִים, כְּשֶׁמָּצְאוּ אוֹתוֹ, רַק נָגַע בָּרִצְפָּה, וְכַאֲשֶׁר מָשַׁכְתָּ אֶת הַקָּצֶה אֶל הַקִּיר, כְּשֶׁהַחֶבֶל מָתוּחַ, הוּא נָגַע בְּנְקֻדָּה שֶׁהִיא רַק שְׁלוֹשָׁה אִינְטְשִׁים מֵעַל הָרִצְפָּה, וְהַקִּיר הָיָה אַרְבָּעָה רֶגֶלִים מֵהַחֶבֶל כְּשֶׁהוּא תָּלוּי בְּמָנוֹחַ. מָה הָאֹרֶךְ שֶׁל הַחֶבֶל מֵהָרִצְפָּה עַד הַתִּקְרָה? מקורות:

  • אחוזות יורקשייר

     

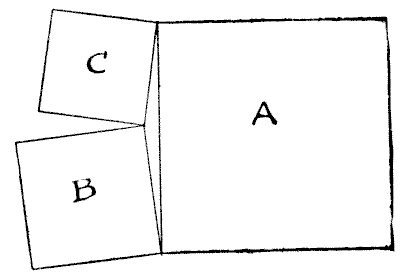
    ביקרתי באחת הערים הגדולות של יורקשייר. בדרכי לתחנת הרכבת ביום עזיבתי, אדם דחף לי עלון, לקחתי אותו לקרון הרכבת וקראתי אותו בשעות הפנאי שלי. הוא הודיע לי ששלוש אחוזות שכנות ביורקשייר מוצעות למכירה. כל אחוזה הייתה בצורת ריבוע, והן הצטרפו זו לזו בפינותיהן, בדיוק כפי שמוצג בתרשים. אחוזה A מכילה בדיוק `370` אקרים, B מכילה `116` אקרים, ו-C `74` אקרים.

    כעת, פיסת הקרקע המשולשת הקטנה התחומה על ידי שלוש האחוזות הריבועיות לא הוצעה למכירה, ומסיבה לא מיוחדת, התעוררתי לסקרנות לגבי שטח החלקה הזו. כמה אקרים היא הכילה?

    מקורות:

  • האחוזה של החוואי וורצל

     

    אציג כעת בעיית שטח נוספת. ההדגמה של התשובה שאציג, אני חושב, תימצא גם מעניינת וגם קלה להבנה.

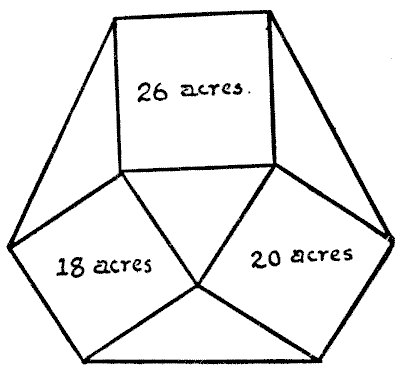
    החוואי וורצל היה הבעלים של שלושה שדות מרובעים כפי שמוצג בתוכנית המצורפת, המכילים בהתאמה `18, 20`, ו-`26` אקרים. כדי להקיף את רכושו בגדר טבעת, הוא קנה את ארבעת השדות המשולשים המפרידים. החידה היא לגלות מה היה אז השטח הכולל של האחוזה שלו.

    מקורות: