גאומטריה, גאומטריה במישור, משפט פיתגורס

משפט פיתגורס הוא קשר יסודי בגאומטריה אוקלידית בין שלוש צלעותיו של משולש ישר-זווית. הוא קובע שריבוע היתר (הצלע שמול הזווית הישרה) שווה לסכום ריבועי שתי הצלעות האחרות (`a^2 + b^2 = c^2`). שאלות כוללות יישום משפט זה למציאת אורכי צלעות.

• שאלה

  נתון חרוט (בעל ציר סימטריה במרכזו, המאונך לבסיסו) שגובהו 6 ובסיסו הוא עיגול בעל רדיוס `sqrt2` . בתוך החרוט חסומה קובייה – היא מונחת על בסיס החרוט וכל קדקודיה העליונים נוגעים בחרוט. מצאו את אורך הצלע של הקובייה. נמקו את תשובתכם.

  

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
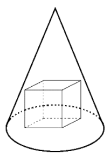  נושאים:

  גאומטריה -> גאומטריה במרחב אלגברה -> משוואות גאומטריה -> גאומטריה במישור -> משפט פיתגורס גאומטריה -> גאומטריה במישור -> משולשים -> דמיון משולשים
  מקורות:
  • אולימפיאדת גיליס, תשע"ו שאלה 2

• שאלה

  על הניצבים ועל היתר של משולש ישר זווית נבנו חצאי מעגלים, כמו שמתואר בציור. איזה שטח גדול יותר – השטח המקווקו או השטח המושחר?

  

  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משולשים גאומטריה -> גאומטריה במישור -> מעגלים גאומטריה -> גאומטריה במישור -> משפט פיתגורס

• שאלה

  לשלומי יש קופסה שטוחה בגודל `5xx5` סנטימטרים. שלומי טוען, שכל מלבן שאפשר לאחסן בקופסה הזאת, כל צלעותיו צריכות להיות קטנות מ-5 סנטימטרים. האם הוא צודק?

  נושאים:

  הוכחה ודוגמה -> בניית דוגמה גאומטריה -> גאומטריה במישור -> משפט פיתגורס

• משולשים ישרי זווית וריבוע

  נתונה כמות גדולה של משולשים ישרי זווית חופפים.

  אורכי הצלעות בכל משולש הן 3 ,4 ו-5.

  כמה משולשים כאלה, לכל היותר, אפשר למקם בתוך ריבוע 20×20 ,כך שהם לא יעלו זה על זה?

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משולשים גאומטריה -> גאומטריה במישור -> משפט פיתגורס
  מקורות:
  • אולימפיאדת גיליס, תשע"ז שאלה 3

• שאלה

  נתון טרפז שווה שוקיים, שאורך השוק שלו a, ואורך האלכסון שלו b, כמו בציור. מצא את הערך הגדול ביותר והקטן ביותר שיכולה לקבל מכפלת הבסיסים (התשובה תלויה ב-`a` וב-`b`).
  

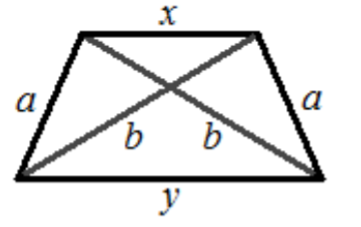  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> מעגלים אלגברה גאומטריה -> גאומטריה במישור -> משפט פיתגורס
  מקורות:
  • מבחני בחירה ל-IMO בישראל, תשע"א, שלב א שאלה 9

• שאלה

  נתון מגדל בצורת תיבה. גובהו 61 מטרים, ובסיסו הוא ריבוע שצלעו 9 מטרים. על הגג,
  בנקודה שנמצאת במרחק של שני מטרים מהקיר הצפוני ושני מטרים מהקיר המערבי, שפכו
  מיץ. נמלה נמצאת בתחתית המגדל, בפינה הדרום מזרחית. לנמלה יש חוש ריח מעולה ולכן
  היא מרגישה איפה בדיוק נשפך המיץ. מהו המרחק המינימלי שהיא צריכה לעבור בשביל
  להגיע לנקודה הזאת? (הנמלה יכול לזחול על הקירות והגג.)
  נושאים:

  גאומטריה -> גאומטריה במרחב גאומטריה -> גאומטריה במישור -> משפט פיתגורס
  מקורות:
  • מבחני בחירה ל-IMO בישראל, תשע"ב, שלב א שאלה 9

• שלושת הכפרים

  יצאתי לדרך אתמול כדי לנסוע במכונית מאייקריפילד לבאטרפורד, אבל בטעות לקחתי את הכביש שעובר דרך צ'יזברי, אשר קרוב יותר לאייקריפילד מאשר לבאטרפורד, והוא שנים עשר מיילים משמאל לכביש הישיר שהייתי צריך לנסוע בו. לאחר שהגעתי לבאטרפורד גיליתי שעברתי שלושים וחמישה מיילים. מהם שלושת המרחקים בין הכפרים הללו, כאשר כל אחד מהם הוא מספר שלם של מיילים? אוסיף ואציין ששלושת הכבישים ישרים לחלוטין.
  נושאים:

  גאומטריה -> גאומטריה במישור -> משולשים אלגברה -> בעיות מילוליות גאומטריה -> גאומטריה במישור -> משפט פיתגורס
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 69

• הנקודה על השולחן

  ילד, שחזר לאחרונה מבית הספר, רצה להציג לאביו את פיקחותו. הוא דחף שולחן עגול גדול לפינת החדר, כפי שמוצג באיור, כך שהוא נגע בשני הקירות, ואז הצביע על כתם דיו בקצה השולחן.

   

  "הנה חידה קטנה בשבילך, אבא," אמר הילד. "הנקודה הזו נמצאת בדיוק שמונה אינץ' מקיר אחד ותשעה אינץ' מהקיר השני. האם תוכל לומר לי מה קוטר השולחן מבלי למדוד אותו?"

  הילד נשמע אומר לחבר, "זה ממש ניצח את אבא;" אבל ידוע שהאב העיר למכר בעיר שהוא פתר את העניין בראשו תוך דקה. אני לעתים קרובות תוהה מי דיבר אמת.

  נושאים:

  גאומטריה -> גאומטריה במישור -> מעגלים אלגברה -> משוואות אלגברה -> בעיות מילוליות גאומטריה -> גאומטריה במישור -> משפט פיתגורס
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 97

• חידת הלחמנייה

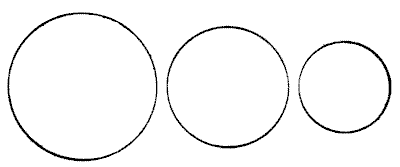  שלושת העיגולים מייצגים שלוש לחמניות, ונדרש פשוט להראות כיצד ניתן לחלק אותן באופן שווה בין ארבעה בנים. יש להתייחס ללחמניות כבעלות עובי שווה לכל אורכן ועובי שווה זו לזו. כמובן, יש לחתוך אותן למספר החלקים המועט ביותר האפשרי. כדי לפשט זאת, אציין את העובדה המפתיעה למדי שדי בחמישה חלקים בלבד, ומכך ניתן יהיה לראות שנער אחד מקבל את חלקו בשני חלקים ושלושת האחרים מקבלים את חלקם בחלק אחד. אני מודע לכך שהצהרה זו "מסגירה" את החידה, אך היא לא אמורה לפגוע בעניינם של אלה שאוהבים לגלות את "הסיבה לכך".
  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> מעגלים גאומטריה -> גאומטריה במישור -> משפט פיתגורס קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 148

• בעיה נוספת של נגר

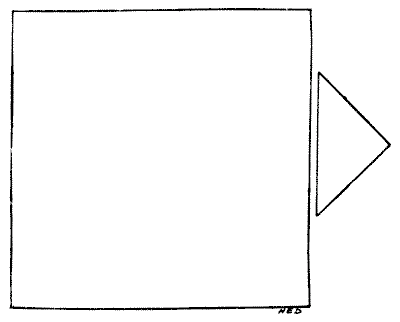  לנגר היו שני חתיכות עץ בצורות ובפרופורציות יחסיות המוצגות בדיאגרמה. הוא רצה לחתוך אותן למספר קטן ככל האפשר של חלקים כך שניתן יהיה לחבר אותם יחד, ללא בזבוז, וליצור משטח שולחן מרובע לחלוטין. איך הוא היה צריך לעשות את זה? אין צורך לתת מידות, כי אם החלק הקטן יותר (שהוא חצי ריבוע) יהיה קצת גדול מדי או קטן מדי, זה לא ישפיע על שיטת הפתרון.
  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משפט פיתגורס קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 152