几何学, 平面几何学, 勾股定理
勾股定理是欧几里得几何中直角三角形三边之间的基本关系。它指出斜边(直角对边)的平方等于其他两边的平方和(`a^2 + b^2 = c^2`)。问题涉及应用此定理来寻找边长。
-
问题
给定一个圆锥(其对称轴位于中心,垂直于其底面),其高度为 6,底面是一个半径为 `sqrt2` 的圆。圆锥内接一个立方体——它位于圆锥的底面上,并且其所有上顶点都接触圆锥。求立方体的边长。解释你的答案。
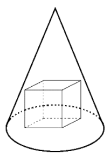 来源:
来源: -
问题
在一个直角三角形的两个直角边和斜边上构造半圆,如图所示。哪个面积更大 – 是阴影部分的面积还是黑色部分的面积?

-
问题
Shlomi 有一个尺寸为 `5xx5` 厘米的扁平盒子。 Shlomi 声称,任何可以放入此盒子的矩形,其所有边都必须小于 5 厘米。 他是对的吗?
-
直角三角形和正方形
给定大量全等的直角三角形。
每个三角形的边长分别为 3、4 和 5。
最多可以在 20×20 的正方形内放置多少个这样的三角形,使它们互不重叠?
来源: