Gillis Mathematical Olympiad, 2015-2016
-
问题 1
尼娜和梅尔同时从他们的家出发,一起去拜访奶奶。从他们家到奶奶家的路线长 3 公里,沿途放置着长椅。
尼娜会在路上的每个长椅上坐下,吃一块饼干。她吃每块饼干的时间都是相同的整数分钟。梅尔也会停下来坐在每条长椅上吃一块饼干。
梅尔吃饼干的时间是尼娜的两倍。此外,已知尼娜的速度是每小时 3 公里,梅尔的速度是每小时 4 公里。
结果表明,梅尔和尼娜同时到达了奶奶家。
路上有多少条长椅?找出所有可能性并解释你的答案
-
问题 2
给定一个圆锥(其对称轴位于中心,垂直于其底面),其高度为 6,底面是一个半径为 `sqrt2` 的圆。圆锥内接一个立方体——它位于圆锥的底面上,并且其所有上顶点都接触圆锥。求立方体的边长。解释你的答案。
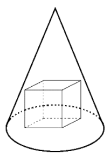
-
问题 3
给定一个正整数N,考虑以下过程:记`S(N)`为N的各位数字之和,取`S(N)`的各位数字之和。重复此操作直到得到一个一位数。称执行上述过程直到得到一位数的次数为N的“深度”。例如,49的深度为`S(49)=13 -> S(13)=4)2`,执行了两次操作(49的深度为2),而45的深度为1。
a) 证明对于任何数N,其深度都是有限的,也就是说,在过程的某个阶段总会得到一个一位数。
b) 记`x(n)`为深度为N的最小数(值最小的数)。求`x(5776)`除以6的余数。请说明你的答案!
c) 求`x(5776) - x(5708)`除以2016的余数。请说明你的答案!
-
问题 4 - 圆与三点
黑板上画着一个圆,圆上有三个点,颜色如下(顺时针方向):绿色、蓝色
和红色。 约拿单在玩以下游戏 – 在每个阶段,他可以执行以下步骤之一:
一) 选择两个颜色不同的相邻点,并在它们之间绘制一个颜色为这两种颜色之一的点
仅限于。
乙) 选择两个颜色相同的相邻点,并在它们之间绘制一个颜色任意的点。
C) 选择三个相邻的点,其中至少有两个颜色相同,然后删除中间的点。约拿单能否达到黑板上只剩下三个点,颜色如下(顺时针方向):蓝色、绿色、红色? 解释你的答案
-
问题 5 - 斐波那契多项式
斐波那契数列定义为 `F_1 = F_2 = 1`,且对于所有整数 `n >= 3`,满足递推公式 `F_n = F_{n-1} + F_{n-2}`。给定自然数 `m,n >= 1`。求最小的次数 `d`,使得存在多项式 `f(x) = a_d x^d + a_{d-1} x^{d-1} + ... + a_1 x + a_0` 满足 `f(k) = F_{m+k}`,对于所有 `k = 0,1,...,n` 成立。请证明你的答案。