אולימפיאדת גיליס, תשע"ו

• שאלה 1

  נינה ומאיר יצאו בו-זמנית יחד מביתם והלכו לבקר את סבתא. המסלול מביתם לבית סבתם הוא באורך 3 ק"מ, ולאורכו ממוקמים ספסלים.

  נינה מתיישבת על כל ספסל בדרך כדי לאכול עוגייה אחת. היא אוכלת כל עוגייה במשך אותו מספר שלם של דקות. גם מאיר עוצר ומתיישב על כל ספסל כדי לאכול עוגייה אחת.

  לוקח למאיר פי שתיים יותר זמן מנינה לאכול עוגייה. כמו כן, ידוע כי נינה הולכת במהירות 3 קמ"ש, ומאיר במהירות 4 קמ"ש.

  התברר כי מאיר ונינה הגיעו בו זמנית לבית של סבתא.

  כמה ספסלים היו בדרך? מצאו את כל האפשרויות ונמקו את תשובתכם

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  אריתמטיקה אלגברה -> משוואות אלגברה -> בעיות מילוליות -> בעיות תנועה

• שאלה 2

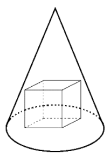
  נתון חרוט (בעל ציר סימטריה במרכזו, המאונך לבסיסו) שגובהו 6 ובסיסו הוא עיגול בעל רדיוס `sqrt2` . בתוך החרוט חסומה קובייה – היא מונחת על בסיס החרוט וכל קדקודיה העליונים נוגעים בחרוט. מצאו את אורך הצלע של הקובייה. נמקו את תשובתכם.

  

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  גאומטריה -> גאומטריה במרחב אלגברה -> משוואות גאומטריה -> גאומטריה במישור -> משפט פיתגורס גאומטריה -> גאומטריה במישור -> משולשים -> דמיון משולשים

• שאלה 3

  בהינתן מספר שלם חיובי N, נתבונן בתהליך הבא: נסמן ב-`S(N)` את סכום הספרות של N ניקח את סכום הספרות של `S(N)`  נחזור על הפעולה שוב ושוב עד שנקבל מספר חד ספרתי נקרא למספר הפעמים שביצענו את התהליך הנ"ל עד שקיבלנו מספר חד-ספרתי: "העומק" של N. לדוגמה, העומק של 49 הוא `S(49)=13 -> S(13)=4)2` , הפעולה בוצעה פעמיים( והעומק של 45 הוא 1.

  א) הוכיחו כי לכל מספר N אכן יש עומק סופי, כלומר, שתמיד יתקבל מספר חד-ספרתי בשלב כלשהו של התהליך.

  ב) נסמן ב-`x(n)` את המספר המינימלי (שערכו הקטן ביותר) בעל עומק N. מצאו את השארית של `x(5776)` בחילוק ב-6 .נמקו את תשובתכם!

  ג) מצאו את השארית של המספר `x(5776) - x(5708)` בחילוק ב-2016 .נמקו את תשובתכם!

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  תורת המספרים -> חשבון השאריות קומבינטוריקה -> אינדוקציה אלגברה -> סדרות -> סדרה חשבונית

• שאלה 4 - מעגל ושלוש נקודות

  על הלוח מצויר מעגל ועליו מסומנות שלוש נקודות בצבעים הבאים (לפי כיוון השעון): ירוק, כחול
  ואדום. יונתן משחק במשחק הבא – בכל שלב הוא יכול לעשות את אחד הצעדים הבאים:
  א) לבחור שתי נקודות סמוכות בעלות צבעים שונים ולצייר ביניהן נקודה באחד משני הצבעים האלו
  בלבד.
  ב) לבחור שתי נקודות סמוכות בעלות צבעים זהים ולצייר ביניהן נקודה בצבע כלשהו.
  ג) לבחור שלוש נקודות סמוכות שלפחות שתיים מהן באותו צבע, ולמחוק את האמצעית.

  האם יונתן יכול להגיע למצב שבו תיוותרנה על הלוח שלוש נקודות בצבעים הבאים (לפי כיוון השעון): כחול, ירוק, אדום? נמקו את תשובתכם

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  קומבינטוריקה -> אינווריאנטים קומבינטוריקה -> צביעות

• שאלה 5 - פולינום פיבונאצ'י

  סדרת פיבונאצ'י מוגדרת לפי `F_1 = F_2 = 1` ונוסחת הנסיגה `F_n = F_{n-1} + F_{n-2}` לכל `n >= 3` שלם. נתונים `m,n >= 1` טבעיים. מצאו את המעלה המינימלית `d` כך שקיים פולינום `f(x) = a_d x^d + a_{d-1} x^{d-1} + ... + a_1 x + a_0` המקיים `f(k) = F_{m+k}` לכל `k = 0,1,...,n` נמקו את תשובתכם

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  אלגברה -> סדרות -> נוסחאות נסיגה