Geometry, Plane Geometry, Angle Calculation

This topic focuses on determining the measures of angles within geometric figures (like polygons, triangles) or those formed by intersecting lines, using fundamental geometric properties and theorems (e.g., sum of angles in a triangle, properties of parallel lines).

• Angles

  Calculate the sum of the marked angles:

  

  Topics:

  Geometry -> Plane Geometry -> Triangles Geometry -> Plane Geometry -> Angle Calculation
  Sources:
  • Young Mathematician Olympiad, 2019-2020, Stage A, Grades 5-6 Question 5

• How many triangles?

  How many triangles are there in the picture?

  

  Topics:

  Geometry -> Plane Geometry -> Triangles Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Geometry -> Plane Geometry -> Angle Calculation Number Theory -> Division
  Sources:
  • Bar-Ilan's weekly mathriddle competition, 2024 Question 7

• Clock Angle

  How many minutes after 7:00 will the angle between the hour and minute hands be exactly one degree for the first time?
  Note: The clock hands move continuously at a constant speed.

  Topics:

  Arithmetic Algebra -> Word Problems -> Motion Problems Geometry -> Plane Geometry -> Angle Calculation
  Sources:
  • Young Mathematician Olympiad, 2020-2021, Stage A, Grades 7-8 Question 3
  • Young Mathematician Olympiad, 2020-2021, Stage A, Grade 9 Question 3

• Cyclic Quadrilaterals

  Given two triangles ACE, BDF
  intersecting at 6 points: G,H,I,J,K,L
  as shown in the figure. It is given that in each of the quadrilaterals
  EFGI, DELH, CDKG, BCJL, ABIK a circle can be inscribed.
  Is it possible that a circle can also be inscribed in quadrilateral FAHJ?
  

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Solid Geometry / Geometry in Space Geometry -> Plane Geometry -> Circles Algebra -> Equations Algebra -> Inequalities Proof and Example -> Proof by Contradiction Geometry -> Plane Geometry -> Angle Calculation
  Sources:
  • Gillis Mathematical Olympiad, 2019-2020 Question 5

• Triangles on Lines

  Six congruent isosceles triangles are arranged as shown in the figure.
  Show that points C, F, and M are collinear.

  

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Plane Geometry -> Angle Calculation Geometry -> Plane Geometry -> Triangles -> Triangle Congruence Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries) -> Parallel Translation / Translation
  Sources:
  • Gillis Mathematical Olympiad, 2018-2019 Question 3

• Hexagonal Tiling

  Given two types of tiles. The shape of each tile of the first type is a regular hexagon with a side of length 1. The shape of each tile of the second type is a regular hexagon with a side of length 2. An unlimited supply of tiles of each type is given. Is it possible to tile the entire plane using these tiles, using both types of tiles?

  Topics:

  Logic -> Reasoning / Logic Proof and Example -> Proof by Contradiction Geometry -> Plane Geometry -> Angle Calculation
  Sources:
  • Grossman Math Olympiad, 2006 Question 4

• DEFECTIVE OBSERVATION

  Our observation of little things is frequently defective, and our memories very liable to lapse. A certain judge recently remarked in a case that he had no recollection whatever of putting the wedding-ring on his wife's finger. Can you correctly answer these questions without having the coins in sight? On which side of a penny is the date given? Some people are so unobservant that, although they are handling the coin nearly every day of their lives, they are at a loss to answer this simple question. If I lay a penny flat on the table, how many other pennies can I place around it, every one also lying flat on the table, so that they all touch the first one? The geometrician will, of course, give the answer at once, and not need to make any experiment. He will also know that, since all circles are similar, the same answer will necessarily apply to any coin. The next question is a most interesting one to ask a company, each person writing down his answer on a slip of paper, so that no one shall be helped by the answers of others. What is the greatest number of three-penny-pieces that may be laid flat on the surface of a half-crown, so that no piece lies on another or overlaps the surface of the half-crown? It is amazing what a variety of different answers one gets to this question. Very few people will be found to give the correct number. Of course the answer must be given without looking at the coins.
  Topics:

  Geometry -> Plane Geometry -> Circles Geometry -> Plane Geometry -> Angle Calculation
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 28

• THE RAILWAY STATION CLOCK

  A clock hangs on the wall of a railway station, `71` ft. `9` in. long and `10` ft. `4` in. high. Those are the dimensions of the wall, not of the clock! While waiting for a train we noticed that the hands of the clock were pointing in opposite directions, and were parallel to one of the diagonals of the wall. What was the exact time?
  Topics:

  Algebra -> Word Problems Arithmetic -> Fractions Geometry -> Plane Geometry -> Angle Calculation
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 65

• THE TETHERED GOAT

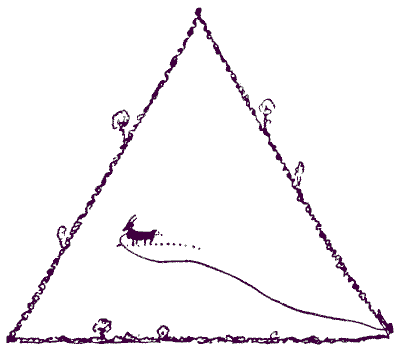  Here is a little problem that everybody should know how to solve. The goat is placed in a half-acre meadow, that is in shape an equilateral triangle. It is tethered to a post at one corner of the field. What should be the length of the tether (to the nearest inch) in order that the goat shall be able to eat just half the grass in the field? It is assumed that the goat can feed to the end of the tether.
  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Triangles Geometry -> Plane Geometry -> Angle Calculation
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 196

• THE YACHT RACE

  Now then, ye land-lubbers, hoist your baby-jib-topsails, break out your spinnakers, ease off your balloon sheets, and get your head-sails set!

  Our race consists in starting from the point at which the yacht is lying in the illustration and touching every one of the sixty-four buoys in fourteen straight courses, returning in the final tack to the buoy from which we start. The seventh course must finish at the buoy from which a flag is flying.

  This puzzle will call for a lot of skilful seamanship on account of the sharp angles at which it will occasionally be necessary to tack. The point of a lead pencil and a good nautical eye are all the outfit that we require.  

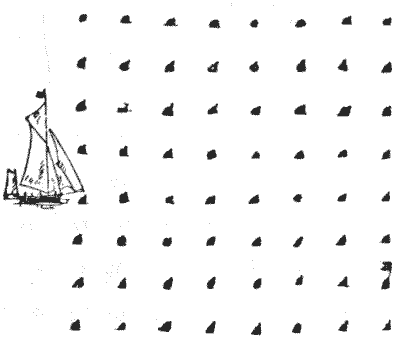
  This is difficult, because of the condition as to the flag-buoy, and because it is a re-entrant tour. But again we are allowed those oblique lines.

  Topics:

  Geometry -> Plane Geometry -> Angle Calculation Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 330