Combinatorics, Combinatorial Geometry, Grid Paper Geometry / Lattice Geometry
This involves geometric problems set on a grid of equally spaced points (a lattice), often where coordinates are integers. Questions might involve finding areas of polygons using grid points (e.g., Pick's Theorem), counting lattice points, or analyzing shapes drawn on grid paper.
-
Orange Star of David
The area of the blue triangle is equal to 1. Calculate the area of the orange Star of David:
Sources:
-
Two Hashes
What is the maximum number of "domino" shapes (rectangles `1 times 2` or `2 times 1`) that can be placed inside the orange shape,
such that they do not overlap and do not extend beyond the boundaries of the shape?
Sources:
-
Largest Perimeter
A polygon with an area of 12 is drawn on grid paper, with all its sides passing through the grid lines. What is the largest possible perimeter of this polygon?
Sources: -
Drawing of a Relation
Given a 5x5 grid divided into 1x1 squares. Two squares are considered related if they are in the same row or column, and the distance between their centers is 2 or 3.
For example, in the drawing, all the squares related to the red square are marked in gray. Sammy receives a blank grid and wants to mark as many squares as possible such that no two of them are related. What is the maximum number of squares he can mark?
Sources:Topics:Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Minimum and Maximum Problems / Optimization Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry- Gillis Mathematical Olympiad, 2018-2019 Question 2
-
Knight's Moves
A knight moves on an infinite grid. It starts at the point (0,0) and must reach
the point (5,27). Assuming it moves in the smallest number of steps required,
how many different possibilities does it have to reach this point?Sources: -
It's Crowded Here!
55 gears are placed on the game board in the shape of a 'pyramid':
10 gears in the bottom row, 9 gears in the row above, and so on.
In this state, the gears cannot rotate freely (convince yourself why!)
Remove gears to allow free movement.
What is the maximum number of gears that can remain on the board so that they can all rotate?
Sources:Topics:Proof and Example -> Constructing an Example / Counterexample Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry- Bar-Ilan's weekly mathriddle competition, 2024 Question 10
-
A PLANTATION PUZZLE
A man had a square plantation of forty-nine trees, but, as will be seen by the omissions in the illustration, four trees were blown down and removed. He now wants to cut down all the remainder except ten trees, which are to be so left that they shall form five straight rows with four trees in every row. Which are the ten trees that he must leave?
Sources:
- Amusements in Mathematics, Henry Ernest Dudeney Question 208
-
TORPEDO PRACTICE
If a fleet of sixteen men-of-war were lying at anchor and surrounded by the enemy, how many ships might be sunk if every torpedo, projected in a straight line, passed under three vessels and sank the fourth? In the diagram we have arranged the fleet in square formation, where it will be seen that as many as seven ships may be sunk (those in the top row and first column) by firing the torpedoes indicated by arrows. Anchoring the fleet as we like, to what extent can we increase this number? Remember that each successive ship is sunk before another torpedo is launched, and that every torpedo proceeds in a different direction; otherwise, by placing the ships in a straight line, we might sink as many as thirteen! It is an interesting little study in naval warfare, and eminently practical—provided the enemy will allow you to arrange his fleet for your convenience and promise to lie still and do nothing!
Sources:
- Amusements in Mathematics, Henry Ernest Dudeney Question 235
-
THE CROSS TARGET
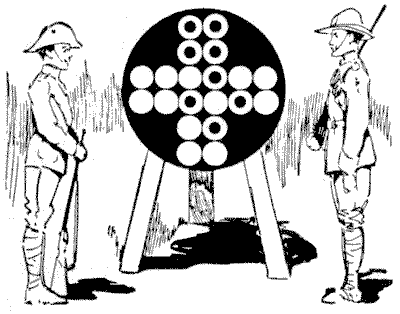In the illustration we have a somewhat curious target designed by an eccentric sharpshooter. His idea was that in order to score you must hit four circles in as many shots so that those four shots shall form a square. It will be seen by the results recorded on the target that two attempts have been successful. The first man hit the four circles at the top of the cross, and thus formed his square. The second man intended to hit the four in the bottom arm, but his second shot, on the left, went too high. This compelled him to complete his four in a different way than he intended. It will thus be seen that though it is immaterial which circle you hit at the first shot, the second shot may commit you to a definite procedure if you are to get your square. Now, the puzzle is to say in just how many different ways it is possible to form a square on the target with four shots.
Sources:Topics:Geometry Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry- Amusements in Mathematics, Henry Ernest Dudeney Question 284
-
LIONS AND CROWNS
The young lady in the illustration is confronted with a little cutting-out difficulty in which the reader may be glad to assist her. She wishes, for some reason that she has not communicated to me, to cut that square piece of valuable material into four parts, all of exactly the same size and shape, but it is important that every piece shall contain a lion and a crown. As she insists that the cuts can only be made along the lines dividing the squares, she is considerably perplexed to find out how it is to be done. Can you show her the way? There is only one possible method of cutting the stuff.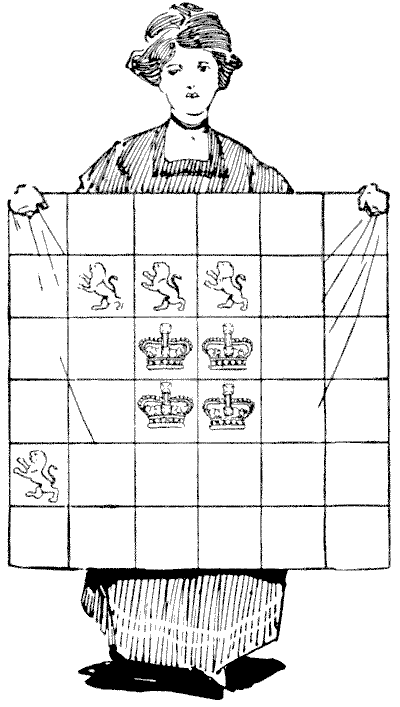
Sources:Topics:Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry- Amusements in Mathematics, Henry Ernest Dudeney Question 289