Combinatorics, Combinatorial Geometry, Grid Paper Geometry / Lattice Geometry

This involves geometric problems set on a grid of equally spaced points (a lattice), often where coordinates are integers. Questions might involve finding areas of polygons using grid points (e.g., Pick's Theorem), counting lattice points, or analyzing shapes drawn on grid paper.

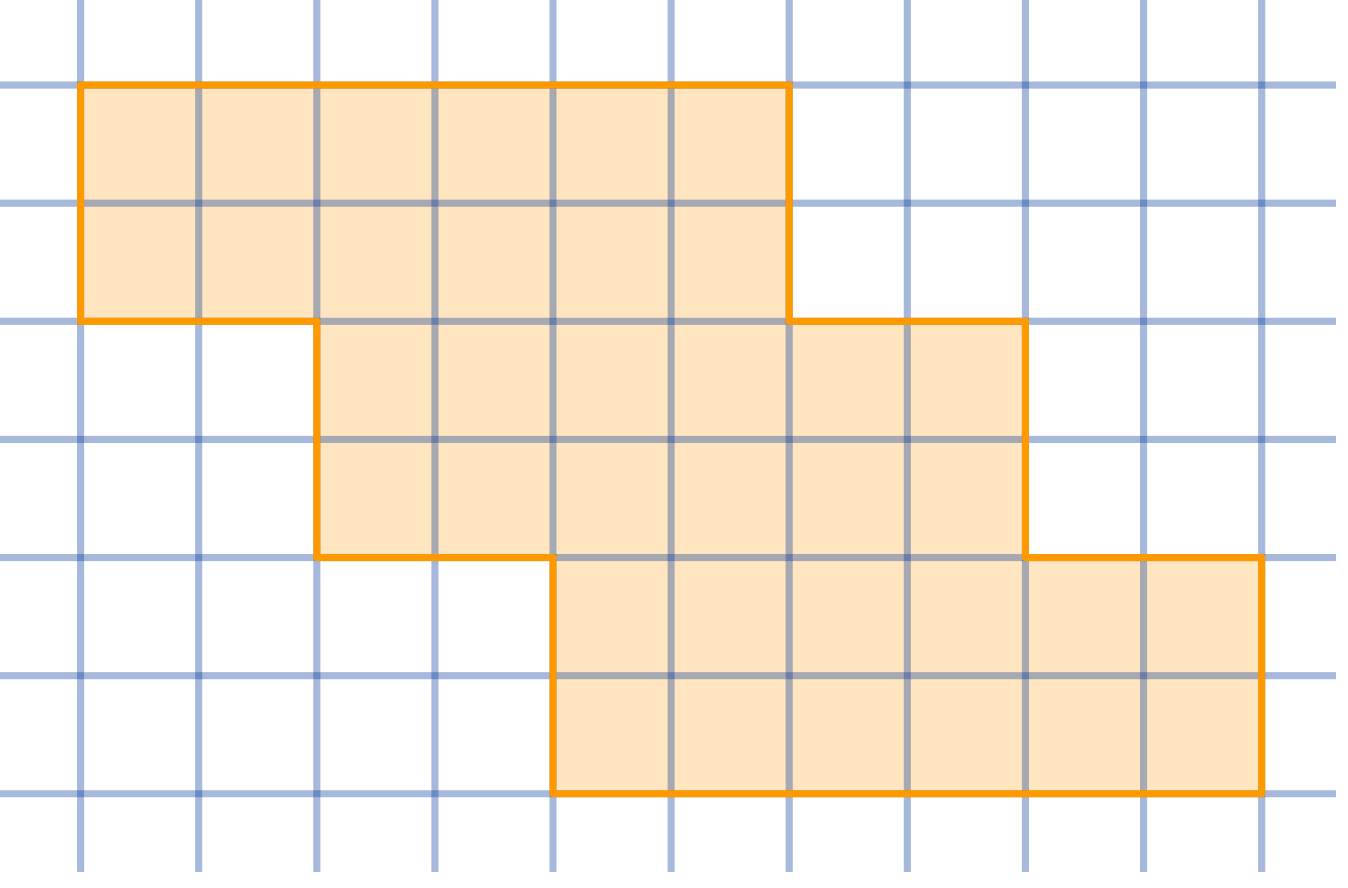
• Question

  Dissect the given shape into four congruent parts:

  ​​​​​​​

  Topics:

  Geometry -> Plane Geometry -> Symmetry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries)

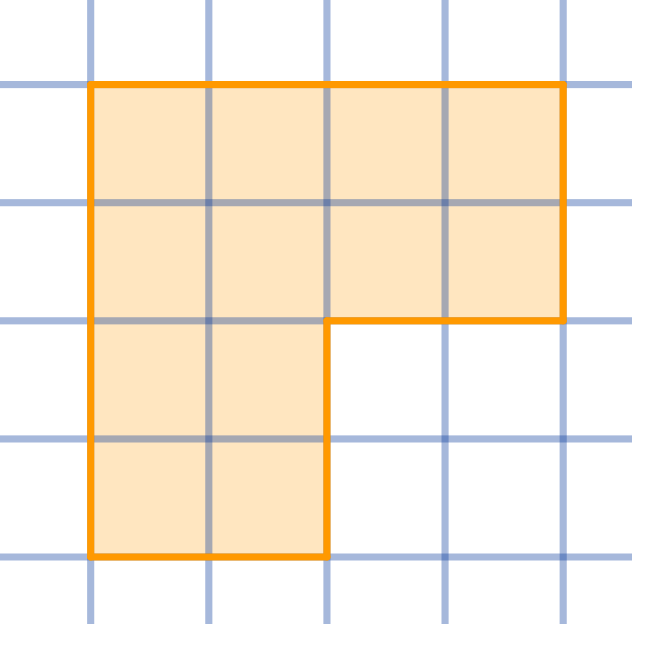
• Question

  Dissect the given shape into four congruent parts:

  

  Topics:

  Geometry -> Plane Geometry -> Symmetry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries)

• Question

  Cut the given shape into eight congruent parts:

  

  Topics:

  Geometry -> Plane Geometry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry

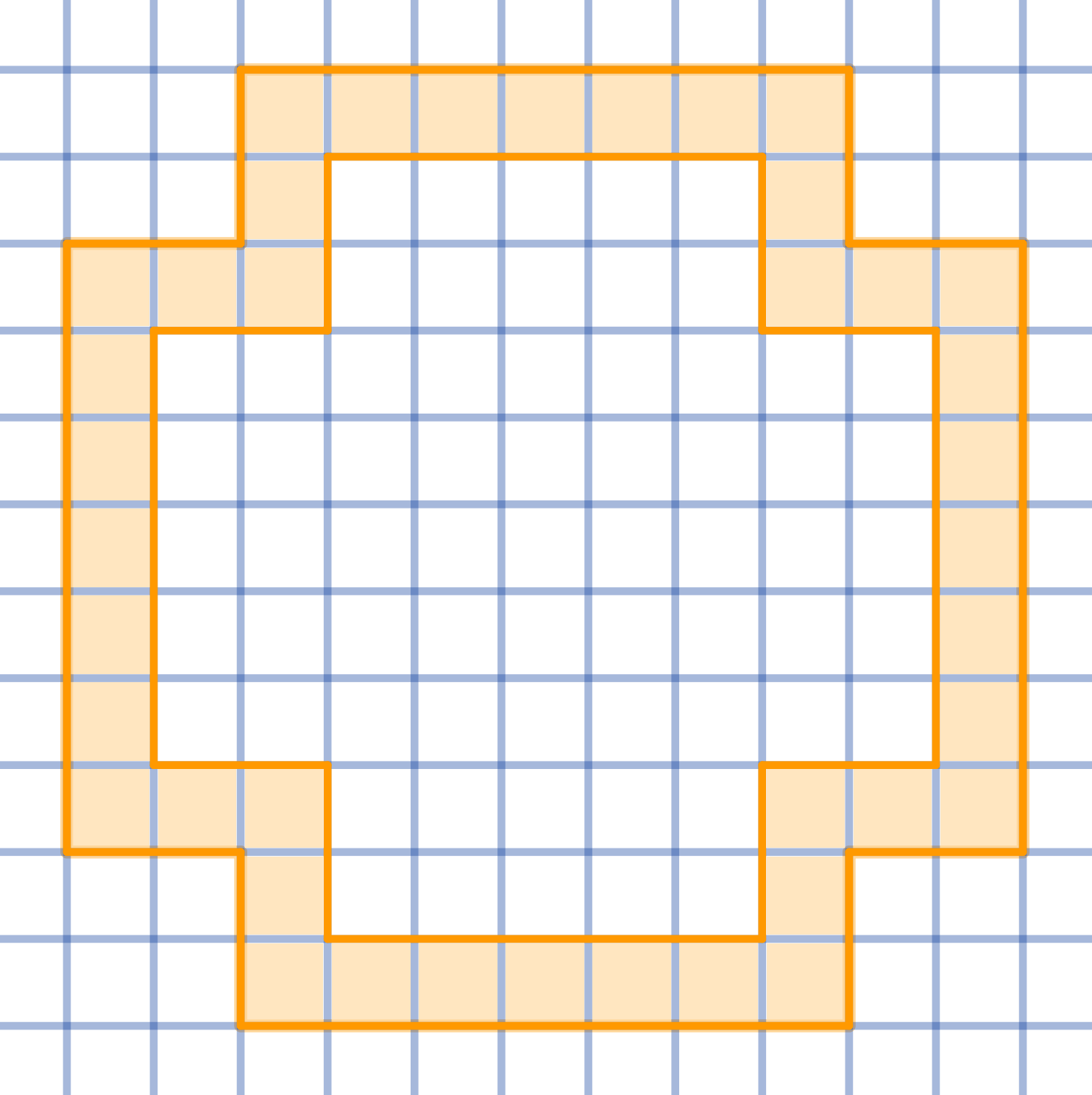
• Question

  Divide the given shape into 16 congruent parts:

  

  Topics:

  Geometry -> Plane Geometry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry

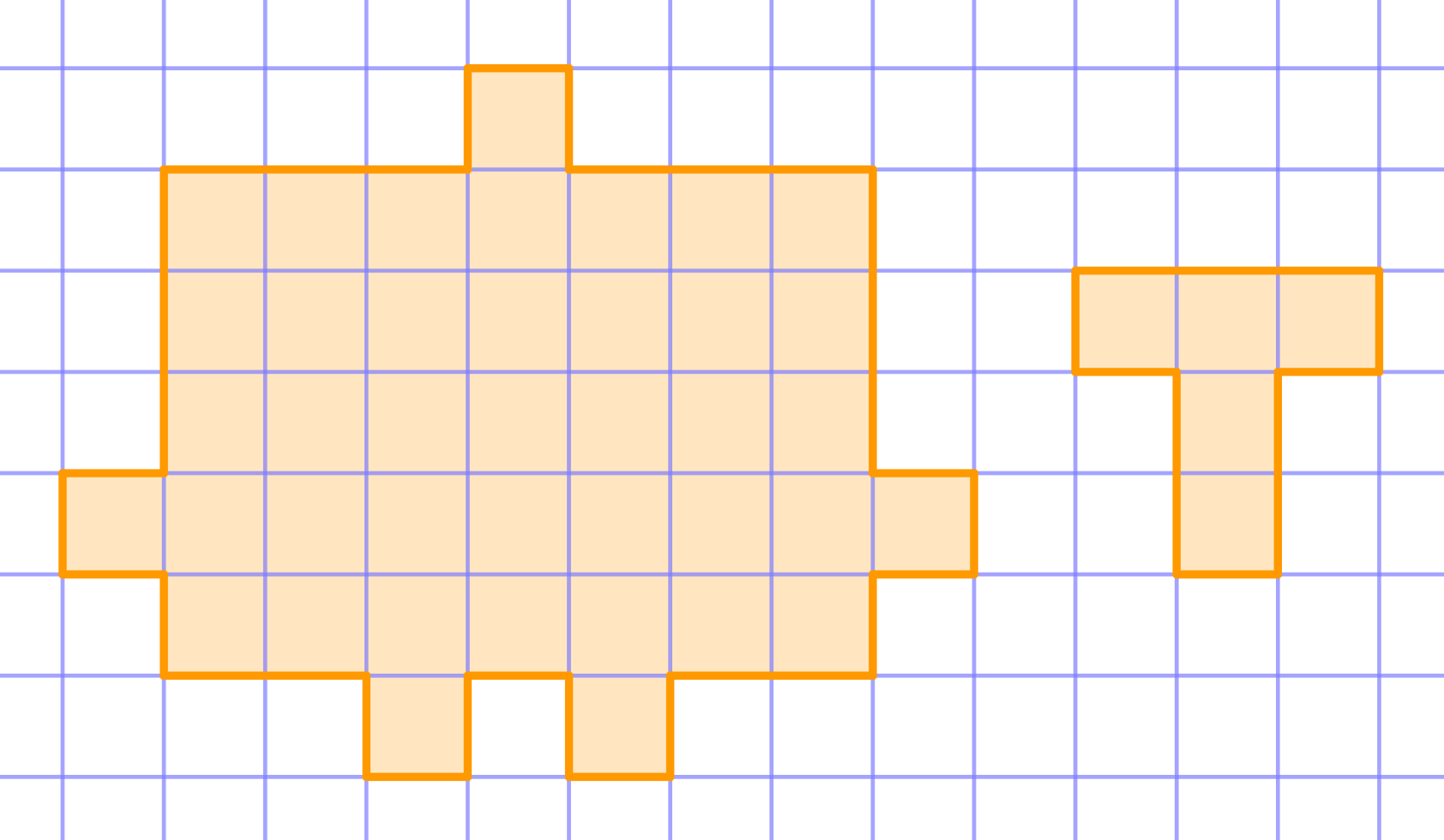
• Question

  Cut the given shape into "T" shapes as shown in the diagram:

  

  Topics:

  Geometry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry

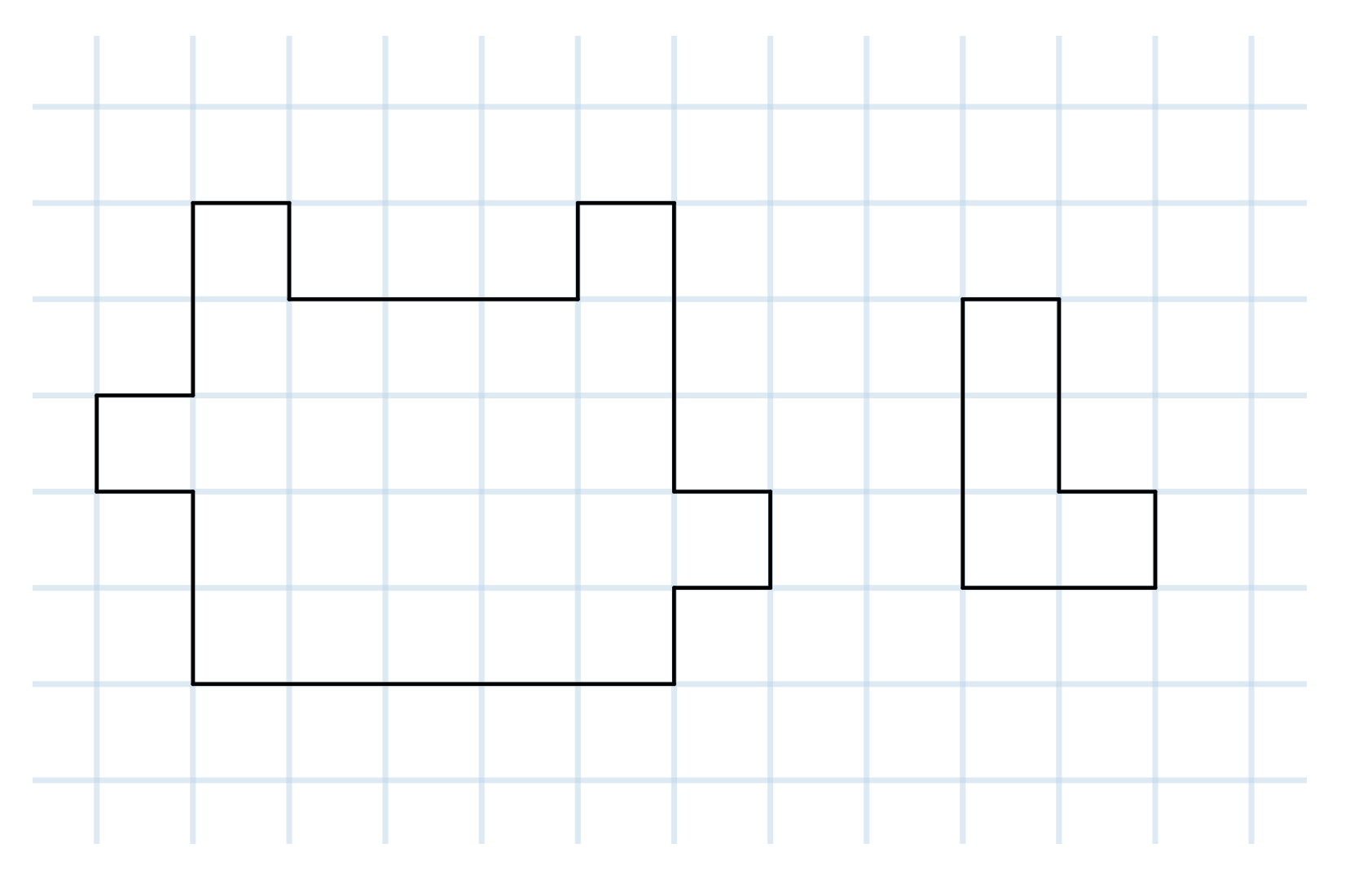
• Question

  Can you cut the shape on the left into six shapes like the shape on the right?

  

  Topics:

  Combinatorics -> Invariants Combinatorics -> Matchings Proof and Example Combinatorics -> Colorings -> Chessboard Coloring Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry

• Question

  What is the maximum number of chess kings that can be placed on an `8xx8` board such that they do not threaten each other?

  Topics:

  Combinatorics -> Pigeonhole Principle Proof and Example -> Constructing an Example / Counterexample Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Minimum and Maximum Problems / Optimization Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry

• Area of the Shape

  Given a grid paper where the area of each square is one unit area. Find the area of the shape (in unit areas)

   

  

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Plane Geometry Geometry -> Area Calculation Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry
  Sources:
  • Young Mathematician Olympiad, 2017-2018, Stage A, Grades 3-4 Question 7

• Cutting

  What is the largest number of rectangles of size `2 times 5`  that can be cut from a `9 times 9` square?

  Topics:

  Geometry -> Area Calculation Proof and Example -> Constructing an Example / Counterexample Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry
  Sources:
  • Young Mathematician Olympiad, 2018-2019, Stage A, Grades 3-4 Question 1
  • Young Mathematician Olympiad, 2018-2019, Stage A, Grades 5-6 Question 1

• The Beaver and the Mole

  There is a plot of land in the shape of a square `4 times 4` divided into cells of `1 times 1`. The beaver wants to build a house on it that occupies 4 cells, which from a top-down view looks like this:

  

  The mole wants to disturb him. For this purpose, it can dig holes, each of which occupies one cell. It is impossible to build on the cells that have become holes. What is the smallest number of holes the mole needs to dig so that the beaver cannot build the house?

   

  Topics:

  Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Colorings Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry
  Sources:
  • Young Mathematician Olympiad, 2018-2019, Final, Grades 3-4 Question 4
  • Young Mathematician Olympiad, 2018-2019, Final, Grades 5-6 Question 2