קומבינטוריקה, כלל המכפלה
עקרון המכפלה הוא עקרון ספירה יסודי: אם יש `n` דרכים לבצע משימה אחת ו-`m` דרכים לבצע משימה אחרת, אז יש `n \times m` דרכים לבצע את שתי המשימות. שאלות כוללות יישום כלל זה לספירת רצפים של בחירות או תוצאות.
-
השרשרת של חוקר העתיקות
לחוקר עתיקות הייתה כמות של חוליות עתיקות מוזרות, אותן לקח לנפח, וביקש ממנו לחבר אותן יחד ליצירת שרשרת ישרה אחת, בתנאי היחיד ששתי החוליות העגולות לא יהיו יחד. האיור הבא מציג את מראה השרשרת ואת צורתה של כל חוליה. כעת, נניח שהבעלים יפריד שוב את החוליות, ואז ייקח אותן לנפח אחר ויחזור בדיוק על ההוראות הקודמות שלו, מה הסיכויים שהחוליות לא יורכבו בדיוק כפי שהורכבו על ידי הנפח הראשון? זכרו שכל חוליה עוקבת יכולה להיות מחוברת לאחרת באחת משתי דרכים, בדיוק כפי שאתם יכולים לשים טבעת על האצבע שלכם בשתי דרכים, או לחבר את האצבעות המורות והאגודלים שלכם בשתי דרכים.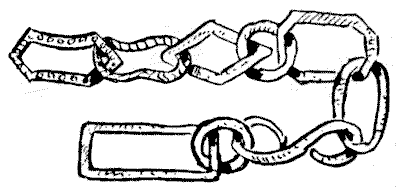 מקורות:
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 282
-
שמונת הצריחים
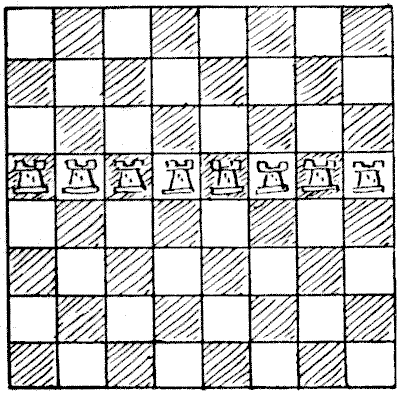 ניתן לראות בדיאגרמה הראשונה שכל משבצת על הלוח מאוכלסת או מותקפת על ידי צריח, וכל צריח "שמור" (אם היו צריחים שחורים ולבנים לסירוגין היינו אומרים "מותקף") על ידי צריח אחר. הצבת שמונת הצריחים על כל שורה או טור תהיה בעלת השפעה זהה. בדיאגרמה `2` כל משבצת שוב מאוכלסת או מותקפת, אך במקרה זה כל צריח אינו שמור. כעת, בכמה דרכים שונות ניתן להציב את שמונת הצריחים על הלוח כך שכל משבצת תהיה מאוכלסת או מותקפת ואף צריח לא יהיה שמור על ידי אחר? אינני רוצה להיכנס לשאלת ההיפוכים והשיקופים בהזדמנות זו, כך שהצבת הצריחים על האלכסון השני תיחשב שונה, וכך גם לגבי חזרות אחרות המתקבלות על ידי סיבוב הלוח.
ניתן לראות בדיאגרמה הראשונה שכל משבצת על הלוח מאוכלסת או מותקפת על ידי צריח, וכל צריח "שמור" (אם היו צריחים שחורים ולבנים לסירוגין היינו אומרים "מותקף") על ידי צריח אחר. הצבת שמונת הצריחים על כל שורה או טור תהיה בעלת השפעה זהה. בדיאגרמה `2` כל משבצת שוב מאוכלסת או מותקפת, אך במקרה זה כל צריח אינו שמור. כעת, בכמה דרכים שונות ניתן להציב את שמונת הצריחים על הלוח כך שכל משבצת תהיה מאוכלסת או מותקפת ואף צריח לא יהיה שמור על ידי אחר? אינני רוצה להיכנס לשאלת ההיפוכים והשיקופים בהזדמנות זו, כך שהצבת הצריחים על האלכסון השני תיחשב שונה, וכך גם לגבי חזרות אחרות המתקבלות על ידי סיבוב הלוח. 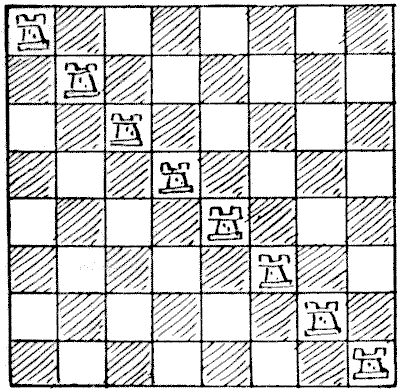 מקורות:נושאים:קומבינטוריקה -> כלל המכפלה
מקורות:נושאים:קומבינטוריקה -> כלל המכפלה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 295
-
ציד אריות
חברי, קפטן פות'ם הול, צייד חיות גדולות ידוע, אומר שאין דבר מלהיב יותר ממפגש עם עדר—להקה—צוות—מִשְׁפָּחָה—נחיל (לקח לי רבע שעה שלמה להיזכר במילה הנכונה, אבל סוף סוף מצאתי אותה)—גאווה של אריות. מדוע מספר אריות נקרא "גאווה," מספר לווייתנים נקרא "בית ספר," ומספר שועלים נקרא "רמייה" הן תעלומות של פילולוגיה שאליהן לא אכנס.
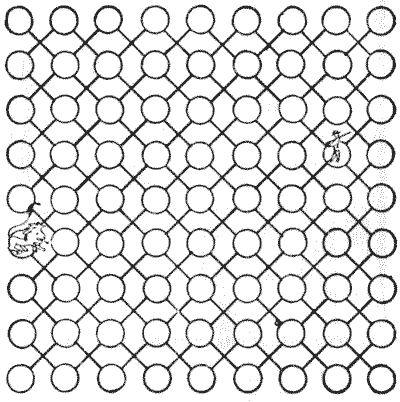
ובכן, הקפטן אומר שאם אריה נמרץ חוצה את דרכך במדבר, זה נהיה תוסס, כי האריה בדרך כלל חיפש את האדם בדיוק כמו שהאדם חיפש את מלך היער. ובכל זאת כשהם נפגשים הם תמיד רבים ונלחמים. קצת התבוננות בסכסוך המצער והמתמשך הזה בין שתי משפחות מכובדות הובילה אותי להבין כמה חישובים לגבי הסבירות שהאדם והאריה יחצו זה את דרכו של זה בג'ונגל. בכל המקרים הללו צריך להתחיל בהנחות מסוימות פחות או יותר שרירותיות. לכן באיור לעיל חשבתי לנכון לייצג את השבילים במדבר בסדר מופתי כזה. למרות שהקפטן מבטיח לי שעקבות האריות בדרך כלל רצים בדרך הזו, יש לי ספקות.
החידה היא פשוט לגלות בכמה דרכים שונות ניתן להציב את האדם והאריה בשני מקומות שונים שאינם על אותו נתיב. על ידי "נתיבים" יש להבין שאני מתייחס רק לקווים המצוירים. לפיכך, למעט ארבע הנקודות הפינתיות, כל לוחם נמצא תמיד בשני נתיבים ולא יותר. ניתן לראות שיש הרבה מקום להתחמק זה מזה במדבר, וזה בדיוק מה שתמיד הבינו.
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 318
-
הַצָּבַת הַלּוּחַ
יש לי לוח שחמט בודד וסט כלי שחמט בודד. בכמה דרכים שונות ניתן להציב את הכלים בצורה נכונה לתחילת משחק? אני מגלה שרוב האנשים טועים בנקודה מסוימת בחישוב.מקורות:נושאים:קומבינטוריקה -> כלל המכפלה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 346
-
שישה חיילים
בכמה דרכים שונות אוכל להניח שישה חיילים על לוח השחמט כך שיהיה מספר זוגי של משבצות לא מאוכלסות בכל שורה ובכל טור? אנחנו לא מתייחסים כאן לאלכסונים כלל, וכל שישה ריבועים מאוכלסים שונים יוצרים פתרון שונה, כך שאיננו צריכים לשלול היפוכים או שיקופים.מקורות:נושאים:קומבינטוריקה -> כלל המכפלה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 358