קומבינטוריקה, כלל המכפלה
עקרון המכפלה הוא עקרון ספירה יסודי: אם יש `n` דרכים לבצע משימה אחת ו-`m` דרכים לבצע משימה אחרת, אז יש `n \times m` דרכים לבצע את שתי המשימות. שאלות כוללות יישום כלל זה לספירת רצפים של בחירות או תוצאות.
-
שאלה
בטבלה בגודל `3×3` אפשר לצבוע כל אחת מהמשבצות בשחור, ואפשר להשאיר אותה לבנה. כמה צביעות כאלו יש?
נושאים:קומבינטוריקה -> כלל המכפלה -
שאלה
בהגרלת "ספורט-לוטו" צריך לנחש תוצאות משחקי כדורגל – בכל משחק ניצחון של הקבוצה הראשונה, ניצחון של הקבוצה השנייה או תיקו, ללא חשיבות לחשבון המדויק. כמה דרכים שונות קיימות למלא כרטיס של ההגרלה הזאת, אם כל כרטיס מכיל `13` משחקים שונים?
נושאים:קומבינטוריקה -> כלל המכפלה -
שאלה
בחברה יש `13` אנשים, כולל המנהל. יום אחד המנהל החליט למנות לו מהעובדים של החברה סגן, ממלא מקום, מזכיר ופקיד. בכמה דרכים שונות הוא יכול לעשות את זה, אם המיומנויות של העובדים לא משפיעות על סוג התפקידים שהם יכולים למלא?
נושאים:קומבינטוריקה -> כלל המכפלה -
שאלה
קניבל לכד `6` אנשים.
א. בכמה דרכים שונות הוא יכול לבחור בן אדם אחד לארוחת בוקר, בן אדם אחד לארוחת צהריים ובן אדם אחד לארוחת ערב?
ב.בכמה דרכים שונות הוא יכול לבחור שלושה בני אדם כדי לשחרר אותם?
נושאים:קומבינטוריקה -> מקדמים בינומיים ומשולש פסקל קומבינטוריקה -> כלל המכפלה תורת המספרים -> חלוקה -
שאלה
בכיתה `30` תלמידים. כל אחד מהם רשאי לצאת לטיול שנתי או להישאר בבית. מהו המספר של הרכבים אפשריים ליציאה לטיול?
נושאים:קומבינטוריקה -> כלל המכפלה -
עוד 2 או 5 אבל לא 3
כמה מספרים חמש ספרתיים מתחלקים ב-2 או ב-5, ולא מתחלקים ב-3?
מקורות:נושאים:תורת המספרים -> חשבון השאריות -> סימני חלוקה -> סימני חלוקה ב-3 וב-9 קומבינטוריקה -> כלל המכפלה -
עוד מספרים בספרות עולות
מירי רושמת את כל המספרים שברישום העשרוני שלהם מופיעות רק הספרות `1, 2, 3, 4, 5, 6`
מקורות:
(לא כל הספרות חייבות להופיע) וכל הספרות שמופיעות רשומות בסדר עולה (למשל 1356 או 124 או 5 אבל לא 162 ולא 1223).
כמה מספרים מירי תרשום? -
צלצול הפעמונים
כתב לי קורספונדנט, שככל הנראה מתעניין מאוד בקמפנולוגיה, ושאל אותי איך עליו לבנות מה שהוא מכנה "צלצול אמיתי ונכון" עבור ארבעה פעמונים. הוא אומר שכל פרמוטציה אפשרית של ארבעת הפעמונים חייבת לצלצל פעם אחת, ופעם אחת בלבד. הוא מוסיף שאף פעמון לא חייב לזוז יותר ממקום אחד בכל פעם, שאף פעמון לא חייב להכות יותר משתי מכות רצופות במקום הראשון או האחרון, ושהשינוי האחרון חייב להיות מסוגל לעבור לראשון. ניתן לראות שתנאים פנטסטיים אלה נשמרים בצליל הקטן לשלושה פעמונים, כדלקמן:—
1 2 3 2 1 3 2 3 1 3 2 1 3 1 2 1 3 2 כיצד עלינו לתת לו פתרון נכון לארבעת הפעמונים שלו?
מקורות:נושאים:קומבינטוריקה -> כלל המכפלה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 268
-
כדורי הזכוכית
מספר קלעים פיקחים שהו שהו באחוזה כפרית, והמארח, כדי לספק קצת בידור, תלה שרשראות של כדורי זכוכית, כפי שמוצג באיור, כדי לירות עליהם. לאחר שכולם העמידו את כישוריהם למבחן מספיק, מישהו שאל את השאלה הבאה: "מהו המספר הכולל של דרכים שונות בהן ניתן לשבור את ששת-עשר הכדורים האלה, אם עלינו תמיד לשבור את הכדור הנמוך ביותר שנותר על כל חוט?" לדוגמה, דרך אחת תהיה לשבור את כל ארבעת הכדורים על כל חוט ברצף, תוך לקיחת החוטים משמאל לימין. דרך נוספת תהיה לשבור תחילה את כל הכדורים הרביעיים על ארבעת החוטים, ואז לשבור את שלושת הנותרים על החוט הראשון, ואז לקחת את הכדורים על שלושת החוטים האחרים לסירוגין מימין לשמאל, וכן הלאה. יש מספר עצום של דרכים שונות (מכיוון שכל וריאציה קטנה של סדר יוצרת דרך שונה) שאדם נוטה להתרשם בתחילה מהקושי הגדול של הבעיה. עם זאת, זה ממש פשוט ברגע שמצאת את השיטה הנכונה לתקוף אותה. כמה דרכים שונות יש?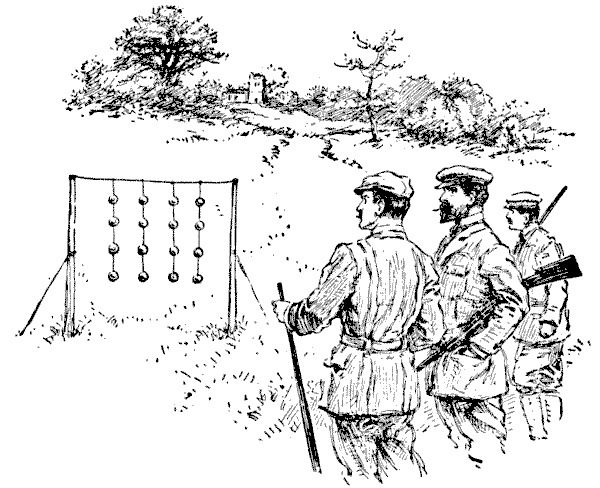 מקורות:נושאים:קומבינטוריקה -> כלל המכפלה
מקורות:נושאים:קומבינטוריקה -> כלל המכפלה- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 270
-
צלבים של מוֹנִים
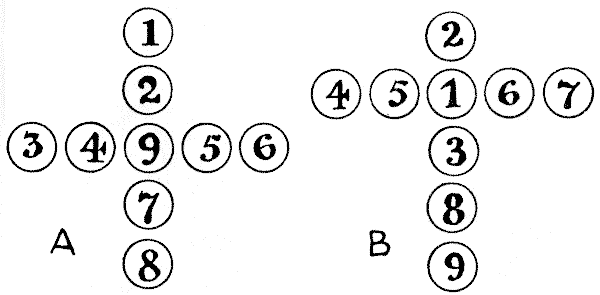
כל מה שאנחנו צריכים לפאזל הזה הם תשעה מוֹנִים, ממוספרים `1, 2, 3, 4, 5, 6, 7, 8` ו-`9`. ניתן לראות באיור A שהם מסודרים כך שיוצרים צלב יווני, ואילו במקרה של B הם יוצרים צלב לטיני. בשני המקרים הקורא יגלה שסכום המספרים באנך של הצלב זהה לסכום המספרים בזרוע האופקית. קל למדי להגיע לסידור כזה בניסוי וטעייה, אך הבעיה היא לגלות בדיוק בכמה דרכים שונות ניתן לעשות זאת בכל מקרה. זכרו שהיפוכים ושיקופים אינם נחשבים כשונים. כלומר, אם תסובבו את הדף הזה תקבלו ארבעה סידורים של הצלב היווני, ואם תסובבו אותו שוב מול מראה תקבלו ארבעה נוספים. אבל את שמונתם אלה מחשיבים כזהים. עכשיו, כמה דרכים שונות יש בכל מקרה?
 מקורות:נושאים:קומבינטוריקה -> כלל המכפלה קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> טבלאות מספריות
מקורות:נושאים:קומבינטוריקה -> כלל המכפלה קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> טבלאות מספריות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 277