גאומטריה, גאומטריה במרחב, פאונים

פאונים הם גופים גאומטריים תלת-ממדיים שפאותיהם הן מצולעים. נושא זה מכסה את תכונותיהם, כגון מספר הפאות, המקצועות והקדקודים, ויחסים כמו נוסחת אוילר (`V-E+F=2`). שאלות עשויות לכלול זיהוי סוגי פאונים וניתוח מבניהם.

• הזבוב על האוקטהדרון

  "תראה," אמר הפרופסור לעמיתו, "אני צופה בזבוב הזה על האוקטהדרון, והוא מגביל את הליכותיו אך ורק לקצוות. מה יכולה להיות הסיבה שלו להימנע מהצדדים?"

  "אולי הוא מנסה לפתור איזושהי בעיית מסלול," הציע השני. "בהנחה שהוא מתחיל מנקודת העליונה, כמה מסלולים שונים יש שבהם הוא יכול ללכת על כל הקצוות, מבלי ללכת פעמיים לאורך אותו קצה בכל מסלול?"

   

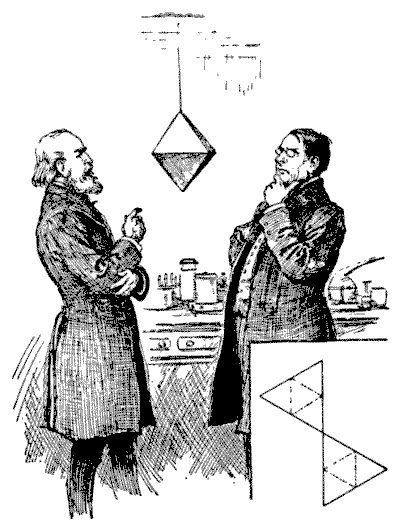
  הבעיה הייתה קשה יותר ממה שהם ציפו, ולאחר שעבדו עליה ברגעי הפנאי במשך מספר ימים התוצאות שלהם לא הסכימו — למעשה, שניהם טעו. אם הקורא מופתע מכישלונם, שינסה בעצמו את החידה הקטנה. אסביר רק שהאוקטהדרון הוא אחד מחמשת הגופים הרגילים, או האפלטוניים, והוא תחום תחת שמונה משולשים שווים ושווי צלעות. אם תגזור את שני חלקי הקרטון בצורה המוצגת בשולי האיור, תגזור חצי דרך לאורך הקווים המקווקווים ואז תכופף אותם ותחבר אותם, תקבל אוקטהדרון מושלם. בכל מסלול על פני כל הקצוות יתגלה שהזבוב חייב להסתיים בנקודת המוצא בראש.

  נושאים:

  קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת הגרפים גאומטריה -> גאומטריה במרחב -> פאונים -> פאונים משוכללים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 245

• הפאזל של האיקוסהדרון

  האיקוסהדרון הוא עוד אחד מחמשת הגופים הרגילים, או האפלטוניים, שכל צדדיהם, זוויותיהם ומישוריהם דומים ושווים. הוא תחום על ידי עשרים משולשים שווי צלעות דומים. אם תגזרו חתיכת קרטון בצורה המוצגת בדיאגרמה הקטנה יותר, ותחתכו חצי עובי לאורך הקווים המקווקווים, היא תתקפל ותיצור איקוסהדרון מושלם.

  ובכן, גוף אפלטוני לא בהכרח מציין גוף שמימי; אבל זה יתאים למטרת הפאזל שלנו אם נניח שיש כוכב לכת ראוי למגורים בצורה הזו. נניח גם שבשל שפע מים, היבשה היחידה נמצאת לאורך הקצוות, ושלתושבים אין ידע בניווט. אם כל אחד מהקצוות האלה באורך `10,000` מיילים, ומטייל בודד ממוקם בקוטב הצפוני (הנקודה הגבוהה ביותר המוצגת), כמה רחוק הוא יצטרך לנסוע לפני שהוא יבקר בכל חלק ראוי למגורים בכוכב הלכת — כלומר, יחצה כל אחד מהקצוות?

  

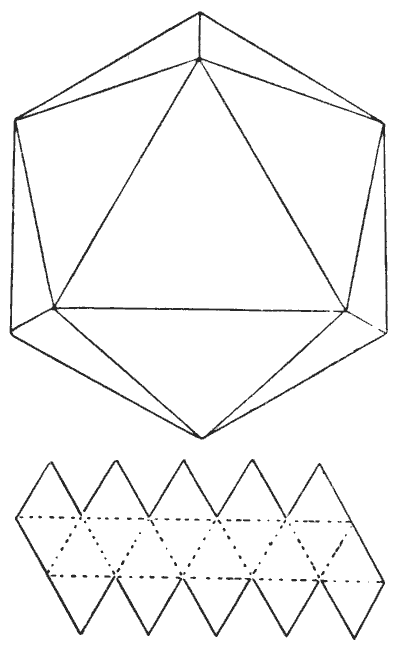  נושאים:

  קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת הגרפים גאומטריה -> גאומטריה במרחב -> פאונים -> פאונים משוכללים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 246