קומבינטוריקה, גאומטריה קומבינטורית, גאומטריה על נייר משבצות
נושא זה כולל בעיות גאומטריות המוגדרות על רשת של נקודות במרווחים שווים (סריג), לעיתים קרובות כאשר הקואורדינטות הן שלמות. שאלות עשויות לכלול מציאת שטחי מצולעים באמצעות נקודות סריג (למשל, משפט פיק), ספירת נקודות סריג, או ניתוח צורות המצוירות על נייר משבצות.
-
ארבעת הקנגורו
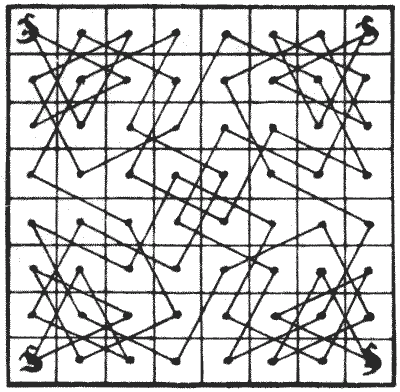 בהציגי בעיה קטנה מחבר העמים, עלי להסביר תחילה שהדיאגרמה מייצגת את שישים וארבעת השדות, כולם מגודרים כראוי זה מזה, של התיישבות אוסטרלית, אם כי אני בקושי צריך לומר שהקרובים שלנו "שם למטה" תמיד כן מסדרים את אדמתם בצורה שיטתית ומדויקת זו. ניתן לראות שבכל אחת מארבע הפינות יש קנגורו. מדוע לקנגורו יש העדפה בולטת לחלקות פינתיות מעולם לא הוסבר בצורה משביעת רצון, וזה לא יהיה במקום לדון בנקודה זו כאן. עלי להוסיף גם כי קנגורו, כפי שידוע, תמיד קופצים במה שאנו מכנים "מהלכי פרש." למעשה, שחקני שחמט כנראה היו מאמצים את המונח הטוב יותר "מהלך קנגורו" אם השחמט לא היה מומצא לפני קנגורו.
בהציגי בעיה קטנה מחבר העמים, עלי להסביר תחילה שהדיאגרמה מייצגת את שישים וארבעת השדות, כולם מגודרים כראוי זה מזה, של התיישבות אוסטרלית, אם כי אני בקושי צריך לומר שהקרובים שלנו "שם למטה" תמיד כן מסדרים את אדמתם בצורה שיטתית ומדויקת זו. ניתן לראות שבכל אחת מארבע הפינות יש קנגורו. מדוע לקנגורו יש העדפה בולטת לחלקות פינתיות מעולם לא הוסבר בצורה משביעת רצון, וזה לא יהיה במקום לדון בנקודה זו כאן. עלי להוסיף גם כי קנגורו, כפי שידוע, תמיד קופצים במה שאנו מכנים "מהלכי פרש." למעשה, שחקני שחמט כנראה היו מאמצים את המונח הטוב יותר "מהלך קנגורו" אם השחמט לא היה מומצא לפני קנגורו.החידה היא פשוטה. בוקר אחד כל קנגורו יצא לקפיצת הבוקר שלו, ובשש עשרה קפיצות פרש רצופות ביקר בחמישה עשר שדות שונים וחזר לפינה שלו. אף שדה לא ביקר על ידי יותר מאחד הקנגורו. הדיאגרמה מראה כיצד הם הסדירו את העניינים. מה שמבקשים מכם לעשות הוא להראות כיצד הם יכלו לבצע את המעשה מבלי שאף קנגורו יחצה את הקו האופקי באמצע הריבוע שמחלק את הלוח לשני חלקים שווים.
מקורות:נושאים:קומבינטוריקה -> תורת הגרפים קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> צביעות -> צביעת שחמט קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 337
-
מסע הפרש הקסום
הנה בעיה שעדיין לא נפתרה, וגם לא הוכחה אי-אפשרותה. שחקו עם הפרש פעם אחת בכל משבצת בלוח השחמט במסע שלם, ספרו את המשבצות לפי סדר הביקור, כך שכאשר תושלם, הריבוע יהיה "קסום," ויסתכם ל-`260` בכל טור, בכל שורה ובכל אחד משני האלכסונים הארוכים. אתן את התשובה הטובה ביותר שהצלחתי להשיג, שבה יש טעות קלה באלכסונים בלבד. האם ניתן למצוא פתרון מושלם? אני משוכנע שאי אפשר, אבל זו רק "דעה נלהבת."
מקורות:נושאים:לוגיקה קומבינטוריקה -> טבלאות מספריות קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 412