Puzzles and Rebuses

This is a general category for brain-teasers that require cleverness, lateral thinking, or pattern recognition. Rebuses are word puzzles using pictures, symbols, or letters to represent words or phrases. Math-related versions might involve numerical or operational clues hidden in a visual format.

Matchstick Puzzles Reconstruct the Exercise / Cryptarithmetic

  • MORE MIXED FRACTIONS

    When I first published my solution to the last puzzle, I was led to attempt the expression of all numbers in turn up to `100` by a mixed fraction containing all the nine digits. Here are twelve numbers for the reader to try his hand at: `13, 14, 15, 16, 18, 20, 27, 36, 40, 69, 72, 94`. Use every one of the nine digits once, and only once, in every case.

    Sources:

  • THE DIGITAL CENTURY

    `1\ 2\ 3\ 4\ 5\ 6\ 7\ 8\ 9 = 100`.

    It is required to place arithmetical signs between the nine figures so that they shall equal `100`. Of course, you must not alter the present numerical arrangement of the figures. Can you give a correct solution that employs (`1`) the fewest possible signs, and (`2`) the fewest possible separate strokes or dots of the pen? That is, it is necessary to use as few signs as possible, and those signs should be of the simplest form. The signs of addition and multiplication (+ and ×) will thus count as two strokes, the sign of subtraction (-) as one stroke, the sign of division (÷) as three, and so on.

    Sources:

  • THE FOUR SEVENS

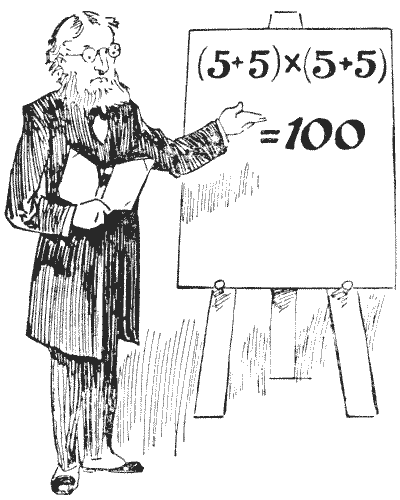    In the illustration Professor Rackbrane is seen demonstrating one of the little posers with which he is accustomed to entertain his class. He believes that by taking his pupils off the beaten tracks he is the better able to secure their attention, and to induce original and ingenious methods of thought. He has, it will be seen, just shown how four `5`'s may be written with simple arithmetical signs so as to represent `100`. Every juvenile reader will see at a glance that his example is quite correct. Now, what he wants you to do is this: Arrange four `7`'s (neither more nor less) with arithmetical signs so that they shall represent `100`. If he had said we were to use four `9`'s we might at once have written `99 9/9`, but the four `7`'s call for rather more ingenuity. Can you discover the little trick?

    Sources:

  • THE CARDBOARD CHAIN

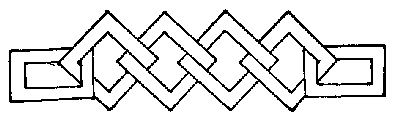    Can you cut this chain out of a piece of cardboard without any join whatever? Every link is solid; without its having been split and afterwards joined at any place. It is an interesting old puzzle that I learnt as a child, but I have no knowledge as to its inventor. Sources:

  • THE EIGHT STICKS

    I have eight sticks, four of them being exactly half the length of the others. I lay every one of these on the table, so that they enclose three squares, all of the same size. How do I do it? There must be no loose ends hanging over. Sources:

  • CHERRIES AND PLUMS

    The illustration is a plan of a cottage as it stands surrounded by an orchard of fifty-five trees. Ten of these trees are cherries, ten are plums, and the remainder apples. The cherries are so planted as to form five straight lines, with four cherry trees in every line. The plum trees are also planted so as to form five straight lines with four plum trees in every line. The puzzle is to show which are the ten cherry trees and which are the ten plums. In order that the cherries and plums should have the most favourable aspect, as few as possible (under the conditions) are planted on the north and east sides of the orchard. Of course in picking out a group of ten trees (cherry or plum, as the case may be) you ignore all intervening trees. That is to say, four trees may be in a straight line irrespective of other trees (or the house) being in between. After the last puzzle this will be quite easy. Sources:

  • THE TEN COINS

    Place ten pennies on a large sheet of paper or cardboard, as shown in the diagram, five on each edge. Now remove four of the coins, without disturbing the others, and replace them on the paper so that the ten shall form five straight lines with four coins in every line. This in itself is not difficult, but you should try to discover in how many different ways the puzzle may be solved, assuming that in every case the two rows at starting are exactly the same.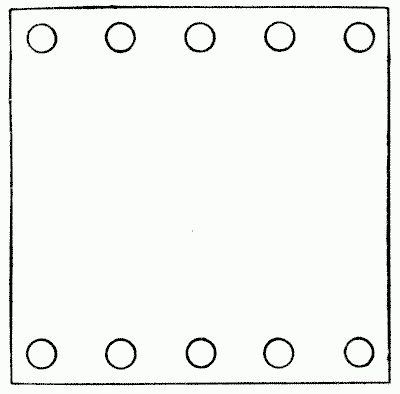 Sources:

  • THE EDUCATED FROGS

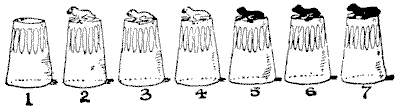    Our six educated frogs have learnt a new and pretty feat. When placed on glass tumblers, as shown in the illustration, they change sides so that the three black ones are to the left and the white frogs to the right, with the unoccupied tumbler at the opposite end—No. `7`. They can jump to the next tumbler (if unoccupied), or over one, or two, frogs to an unoccupied tumbler. The jumps can be made in either direction, and a frog may jump over his own or the opposite colour, or both colours. Four suecessive specimen jumps will make everything quite plain: `4` to `1, 5` to `4, 3` to `5, 6` to `3`. Can you show how they do it in ten jumps? Sources:

  • THE TWICKENHAM PUZZLE

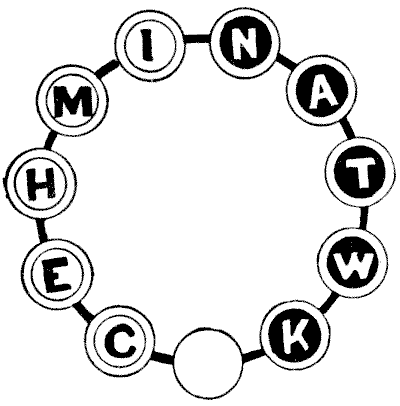    In the illustration we have eleven discs in a circle. On five of the discs we place white counters with black letters—as shown—and on five other discs the black counters with white letters. The bottom disc is left vacant. Starting thus, it is required to get the counters into order so that they spell the word "Twickenham" in a clockwise direction, leaving the vacant disc in the original position. The black counters move in the direction that a clock-hand revolves, and the white counters go the opposite way. A counter may jump over one of the opposite colour if the vacant disc is next beyond. Thus, if your first move is with K, then C can jump over K. If then K moves towards E, you may next jump W over C, and so on. The puzzle may be solved in twenty-six moves. Remember a counter cannot jump over one of its own colour. Sources:

  • THE VICTORIA CROSS PUZZLE

     

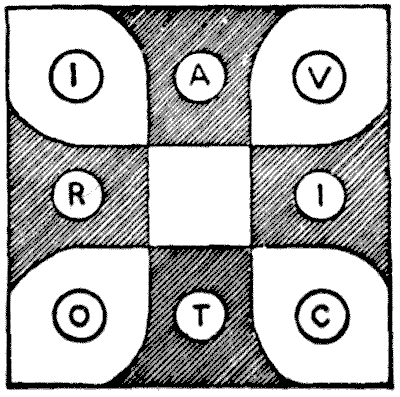
    The puzzle-maker is peculiarly a "snapper-up of unconsidered trifles," and his productions are often built up with the slenderest materials. Trivialities that might entirely escape the observation of others, or, if they were observed, would be regarded as of no possible moment, often supply the man who is in quest of posers with a pretty theme or an idea that he thinks possesses some "basal value."

    When seated opposite to a lady in a railway carriage at the time of Queen Victoria's Diamond Jubilee, my attention was attracted to a brooch that she was wearing. It was in the form of a Maltese or Victoria Cross, and bore the letters of the word VICTORIA. The number and arrangement of the letters immediately gave me the suggestion for the puzzle which I now present.

    The diagram, it will be seen, is composed of nine divisions. The puzzle is to place eight counters, bearing the letters of the word VICTORIA, exactly in the manner shown, and then slide one letter at a time from black to white and white to black alternately, until the word reads round in the same direction, only with the initial letter V on one of the black arms of the cross. At no time may two letters be in the same division. It is required to find the shortest method.

    Leaping moves are, of course, not permitted. The first move must obviously be made with A, I, T, or R. Supposing you move T to the centre, the next counter played will be O or C, since I or R cannot be moved. There is something a little remarkable in the solution of this puzzle which I will explain.

    Sources: