Puzzles and Rebuses

This is a general category for brain-teasers that require cleverness, lateral thinking, or pattern recognition. Rebuses are word puzzles using pictures, symbols, or letters to represent words or phrases. Math-related versions might involve numerical or operational clues hidden in a visual format.

• THE SIXTEEN SHEEP

  Here is a new puzzle with matches and counters or coins. In the illustration the matches represent hurdles and the counters sheep. The sixteen hurdles on the outside, and the sheep, must be regarded as immovable; the puzzle has to do entirely with the nine hurdles on the inside. It will be seen that at present these nine hurdles enclose four groups of `8, 3, 3`, and `2` sheep. The farmer requires to readjust some of the hurdles so as to enclose `6, 6`, and `4` sheep. Can you do it by only replacing two hurdles? When you have succeeded, then try to do it by replacing three hurdles; then four, five, six, and seven in succession. Of course, the hurdles must be legitimately laid on the dotted lines, and no such tricks are allowed as leaving unconnected ends of hurdles, or two hurdles placed side by side, or merely making hurdles change places. In fact, the conditions are so simple that any farm labourer will understand it directly.
  Topics:

  Puzzles and Rebuses -> Matchstick Puzzles
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 275

• A mistake in the exercise

  Prove that there is an error in the following multiplication problem:

  \(\begin{array}& & & * & * & * & 2 & 7 \\ \times & & & & & * & * \\ \hline & * & * & * & * & * & 6 \\ + & * & * & * & * & * & \\ \hline & * & * & * & * & 4 & 6 \end{array}\)

  Topics:

  Arithmetic Logic -> Reasoning / Logic Proof and Example -> Proof by Contradiction Number Theory -> Division Puzzles and Rebuses -> Reconstruct the Exercise / Cryptarithmetic
  Sources:
  • Beno Arbel Olympiad, 2013, Grade 7 Question 4

• Question

  In the following arithmetic puzzle, different digits have been replaced by different letters, and identical digits – by identical letters. Reconstruct the puzzle:

  `BAOxxBAxxB=2002`

  Topics:

  Arithmetic Algebra -> Equations Algebra -> Inequalities Logic -> Reasoning / Logic Number Theory -> Prime Numbers -> Prime Factorization Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Puzzles and Rebuses -> Reconstruct the Exercise / Cryptarithmetic

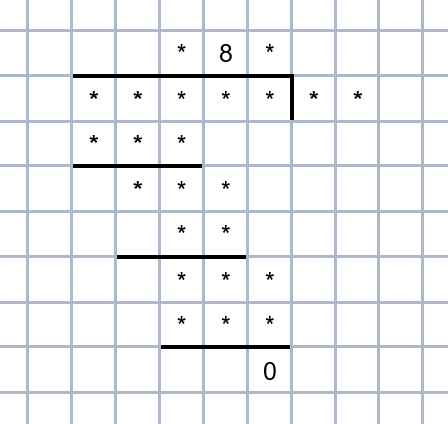
• Reconstruct the Exercise

  Reconstruct the digits in the following exercise:

  

  Topics:

  Arithmetic Number Theory -> Division Puzzles and Rebuses -> Reconstruct the Exercise / Cryptarithmetic

• Baobab

  In the following exercise, identical digits have been replaced with identical letters, and different digits have been replaced with different letters. Reconstruct the exercise.

  `BAOxxBAxxB = 2002`

   

   

   

   

  Topics:

  Arithmetic Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules Logic -> Reasoning / Logic Number Theory -> Prime Numbers -> Prime Factorization Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Puzzles and Rebuses -> Reconstruct the Exercise / Cryptarithmetic

• Letter Replacement

  Each letter represents a different digit; whenever a specific letter appears, it is necessarily the same digit.

  Find `B-E/2`

  Given: `AB*C=DE`

  And also `F^D=GF`

  Show hint

  Log in here to receive the hint
  Topics:

  Number Theory -> Prime Numbers Arithmetic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Number Theory -> Division Puzzles and Rebuses -> Reconstruct the Exercise / Cryptarithmetic

• ABC

  In the following exercise, different digits have been replaced with different letters, and identical digits have been replaced with identical digits. Find the three-digit number ABC

  `ABC - A -B-C=DCA`

  Topics:

  Puzzles and Rebuses -> Reconstruct the Exercise / Cryptarithmetic
  Sources:
  • Young Mathematician Olympiad, 2018-2019, Stage B, Grades 5-6 Question 2

• SLV LVS BLS

  In the following expression, different letters represent different digits, and identical letters represent identical digits:

  SLV = LVS + BLS

  Find the number SLV.

  Topics:

  Arithmetic Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules -> Divisibility Rule by 11 Algebra -> Equations Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Puzzles and Rebuses -> Reconstruct the Exercise / Cryptarithmetic
  Sources:
  • Young Mathematician Olympiad, 2019-2020, Stage B, Grades 5-6 Question 3

• Question

  In the following addition problem, different shapes replace different digits, and identical shapes replace identical digits:

  `triangle square triangle square triangle+ square triangle square triangle square = o+ triangle triangle triangle triangle o+`

  What is the result of the addition?

  Topics:

  Arithmetic Algebra -> Equations Logic -> Reasoning / Logic Puzzles and Rebuses -> Reconstruct the Exercise / Cryptarithmetic
  Sources:
  • Young Mathematician Olympiad, 2020-2021, Stage A, Grades 3-4 Question 3

• The Disguised Digits

  In the following division exercise, (almost) all the digits are disguised!

  What is the dividend?

  \(\begin{align*} &\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }**\text{ }8**\\ &\overline{* * * * * * *\text{ } *}| * *\text{ } *\\ &\underline{\text{ }\text{ }* *\text{ } *}\\ &\text{ }\text{ }\text{ }\text{ }\text{ }* * * *\\ &\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\underline{\text{ }\text{ }* *\text{ } *}\\ &\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }* * * *\\ &\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\underline{* * *\text{ } *}\\ \end{align*}\)

  Topics:

  Arithmetic Number Theory -> Division Puzzles and Rebuses -> Reconstruct the Exercise / Cryptarithmetic
  Sources:
  • Bar-Ilan's weekly mathriddle competition, 2024 Question 8