Puzzles and Rebuses

This is a general category for brain-teasers that require cleverness, lateral thinking, or pattern recognition. Rebuses are word puzzles using pictures, symbols, or letters to represent words or phrases. Math-related versions might involve numerical or operational clues hidden in a visual format.

Matchstick Puzzles Reconstruct the Exercise / Cryptarithmetic

  • THE GRAND LAMA'S PROBLEM

    Once upon a time there was a Grand Lama who had a chessboard made of pure gold, magnificently engraved, and, of course, of great value. Every year a tournament was held at Lhassa among the priests, and whenever any one beat the Grand Lama it was considered a great honour, and his name was inscribed on the back of the board, and a costly jewel set in the particular square on which the checkmate had been given. After this sovereign pontiff had been defeated on four occasions he died—possibly of chagrin.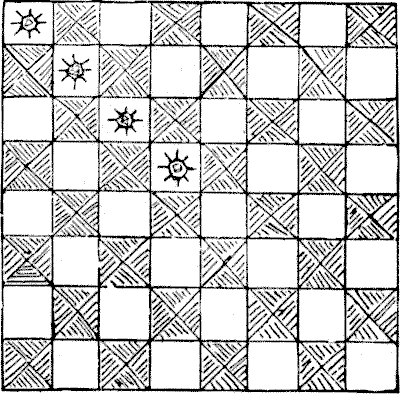 Now the new Grand Lama was an inferior chess-player, and preferred other forms of innocent amusement, such as cutting off people's heads. So he discouraged chess as a degrading game, that did not improve either the mind or the morals, and abolished the tournament summarily. Then he sent for the four priests who had had the effrontery to play better than a Grand Lama, and addressed them as follows: "Miserable and heathenish men, calling yourselves priests! Know ye not that to lay claim to a capacity to do anything better than my predecessor is a capital offence? Take that chessboard and, before day dawns upon the torture chamber, cut it into four equal parts of the same shape, each containing sixteen perfect squares, with one of the gems in each part! If in this you fail, then shall other sports be devised for your special delectation. Go!" The four priests succeeded in their apparently hopeless task. Can you show how the board may be divided into four equal parts, each of exactly the same shape, by cuts along the lines dividing the squares, each part to contain one of the gems? Sources:

  • THE CHESSBOARD SENTENCE

     

    I once set myself the amusing task of so dissecting an ordinary chessboard into letters of the alphabet that they would form a complete sentence. It will be seen from the illustration that the pieces assembled give the sentence, "CUT THY LIFE," with the stops between. The ideal sentence would, of course, have only one full stop, but that I did not succeed in obtaining.

    The sentence is an appeal to the transgressor to cut himself adrift from the evil life he is living. Can you fit these pieces together to form a perfect chessboard?

    Sources:

  • THE EIGHT QUEENS

    The queen is by far the strongest piece on the chessboard. If you place her on one of the four squares in the centre of the board, she attacks no fewer than twenty-seven other squares; and if you try to hide her in a corner, she still attacks twenty-one squares. Eight queens may be placed on the board so that no queen attacks another, and it is an old puzzle (first proposed by Nauck in `1850`, and it has quite a little literature of its own) to discover in just how many different ways this may be done. I show one way in the diagram, and there are in all twelve of these fundamentally different ways. These twelve produce ninety-two ways if we regard reversals and reflections as different. The diagram is in a way a symmetrical arrangement. If you turn the page upside down, it will reproduce itself exactly; but if you look at it with one of the other sides at the bottom, you get another way that is not identical. Then if you reflect these two ways in a mirror you get two more ways. Now, all the other eleven solutions are non-symmetrical, and therefore each of them may be presented in eight ways by these reversals and reflections. It will thus be seen why the twelve fundamentally different solutions produce only ninety-two arrangements, as I have said, and not ninety-six, as would happen if all twelve were non-symmetrical. It is well to have a clear understanding on the matter of reversals and reflections when dealing with puzzles on the chessboard. Can the reader place the eight queens on the board so that no queen shall attack another and so that no three queens shall be in a straight line in any oblique direction? Another glance at the diagram will show that this arrangement will not answer the conditions, for in the two directions indicated by the dotted lines there are three queens in a straight line. There is only one of the twelve fundamental ways that will solve the puzzle. Can you find it? Sources:

  • THE EIGHT STARS

    The puzzle in this case is to place eight stars in the diagram so that no star shall be in line with another star horizontally, vertically, or diagonally. One star is already placed, and that must not be moved, so there are only seven for the reader now to place. But you must not place a star on any one of the shaded squares. There is only one way of solving this little puzzle. Sources:

  • UNDER THE VEIL

    If the reader will examine the above diagram, he will see that I have so placed eight V's, eight E's, eight I's, and eight L's in the diagram that no letter is in line with a similar one horizontally, vertically, or diagonally. Thus, no V is in line with another V, no E with another E, and so on. There are a great many different ways of arranging the letters under this condition. The puzzle is to find an arrangement that produces the greatest possible number of four-letter words, reading upwards and downwards, backwards and forwards, or diagonally. All repetitions count as different words, and the five variations that may be used are: VEIL, VILE, LEVI, LIVE, and EVIL.

    This will be made perfectly clear when I say that the above arrangement scores eight, because the top and bottom row both give VEIL; the second and seventh columns both give VEIL; and the two diagonals, starting from the L in the 5th row and E in the 8th row, both give LIVE and EVIL. There are therefore eight different readings of the words in all.

    This difficult word puzzle is given as an example of the use of chessboard analysis in solving such things. Only a person who is familiar with the "Eight Queens" problem could hope to solve it.

    Sources:

  • THE COLOURED COUNTERS

    The diagram represents twenty-five coloured counters, Red, Blue, Yellow, Orange, and Green (indicated by their initials), and there are five of each colour, numbered `1, 2, 3, 4`, and `5`. The problem is so to place them in a square that neither colour nor number shall be found repeated in any one of the five rows, five columns, and two diagonals. Can you so rearrange them? Sources:

  • THE FORTY-NINE COUNTERS

    Can you rearrange the above forty-nine counters in a square so that no letter, and also no number, shall be in line with a similar one, vertically, horizontally, or diagonally? Here I, of course, mean in the lines parallel with the diagonals, in the chessboard sense. Sources:

  • THE FIVE CRESCENTS OF BYZANTIUM

    When Philip of Macedon, the father of Alexander the Great, found himself confronted with great difficulties in the siege of Byzantium, he set his men to undermine the walls. His desires, however, miscarried, for no sooner had the operations been begun than a crescent moon suddenly appeared in the heavens and discovered his plans to his adversaries. The Byzantines were naturally elated, and in order to show their gratitude they erected a statue to Diana, and the crescent became thenceforward a symbol of the state. In the temple that contained the statue was a square pavement composed of sixty-four large and costly tiles. These were all plain, with the exception of five, which bore the symbol of the crescent. These five were for occult reasons so placed that every tile should be watched over by (that is, in a straight line, vertically, horizontally, or diagonally with) at least one of the crescents. The arrangement adopted by the Byzantine architect was as follows:—

     

    Now, to cover up one of these five crescents was a capital offence, the death being something very painful and lingering. But on a certain occasion of festivity it was necessary to lay down on this pavement a square carpet of the largest dimensions possible, and I have shown in the illustration by dark shading the largest dimensions that would be available.

    The puzzle is to show how the architect, if he had foreseen this question of the carpet, might have so arranged his five crescent tiles in accordance with the required conditions, and yet have allowed for the largest possible square carpet to be laid down without any one of the five crescent tiles being covered, or any portion of them.

    Sources:

  • QUEENS AND BISHOP PUZZLE

    It will be seen that every square of the board is either occupied or attacked. The puzzle is to substitute a bishop for the rook on the same square, and then place the four queens on other squares so that every square shall again be either occupied or attacked.

    Sources:

  • THE SOUTHERN CROSS

     

    In the above illustration we have five Planets and eighty-one Fixed Stars, five of the latter being hidden by the Planets. It will be found that every Star, with the exception of the ten that have a black spot in their centres, is in a straight line, vertically, horizontally, or diagonally, with at least one of the Planets. The puzzle is so to rearrange the Planets that all the Stars shall be in line with one or more of them.

    In rearranging the Planets, each of the five may be moved once in a straight line, in either of the three directions mentioned. They will, of course, obscure five other Stars in place of those at present covered.

    Sources: