Combinatorics

Combinatorics is the art of counting. It deals with selections, arrangements, and combinations of objects. Questions involve determining the number of ways to perform tasks, arrange items (permutations), or choose subsets (combinations), often using principles like the product rule and sum rule.

Pigeonhole Principle Double Counting Binomial Coefficients and Pascal's Triangle Product Rule / Rule of Product Graph Theory Matchings Induction (Mathematical Induction) Game Theory Combinatorial Geometry Invariants Case Analysis / Checking Cases Processes / Procedures Number Tables Colorings

• THE KENNEL PUZZLE

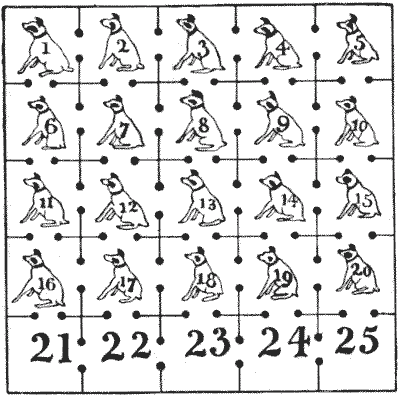  A man has twenty-five dog kennels all communicating with each other by doorways, as shown in the illustration. He wishes to arrange his twenty dogs so that they shall form a knight's string from dog No. `1` to dog No. `20`, the bottom row of five kennels to be left empty, as at present. This is to be done by moving one dog at a time into a vacant kennel. The dogs are well trained to obedience, and may be trusted to remain in the kennels in which they are placed, except that if two are placed in the same kennel together they will fight it out to the death. How is the puzzle to be solved in the fewest possible moves without two dogs ever being together?
  Topics:

  Combinatorics -> Game Theory
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 344

• THE TWO PAWNS

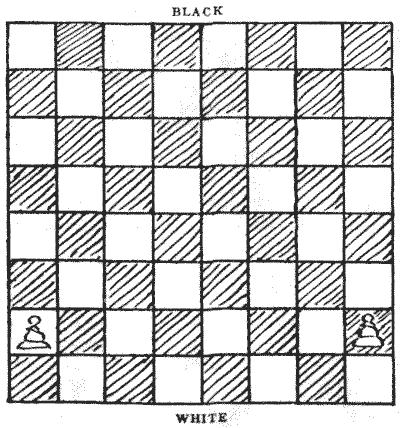  Here is a neat little puzzle in counting. In how many different ways may the two pawns advance to the eighth square? You may move them in any order you like to form a different sequence. For example, you may move the Q R P (one or two squares) first, or the K R P first, or one pawn as far as you like before touching the other. Any sequence is permissible, only in this puzzle as soon as a pawn reaches the eighth square it is dead, and remains there unconverted. Can you count the number of different sequences? At first it will strike you as being very difficult, but I will show that it is really quite simple when properly attacked.

  Topics:

  Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 345

• SETTING THE BOARD

  I have a single chessboard and a single set of chessmen. In how many different ways may the men be correctly set up for the beginning of a game? I find that most people slip at a particular point in making the calculation.
  Topics:

  Combinatorics -> Product Rule / Rule of Product
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 346

• COUNTING THE RECTANGLES

  Can you say correctly just how many squares and other rectangles the chessboard contains? In other words, in how great a number of different ways is it possible to indicate a square or other rectangle enclosed by lines that separate the squares of the board?
  Topics:

  Combinatorics Geometry -> Area Calculation Number Theory -> Triangular Numbers
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 347

• STALEMATE

  Some years ago the puzzle was proposed to construct an imaginary game of chess, in which White shall be stalemated in the fewest possible moves with all the thirty-two pieces on the board. Can you build up such a position in fewer than twenty moves?
  Topics:

  Combinatorics -> Game Theory Logic -> Reasoning / Logic Puzzles and Rebuses
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 349

• THE FORSAKEN KING

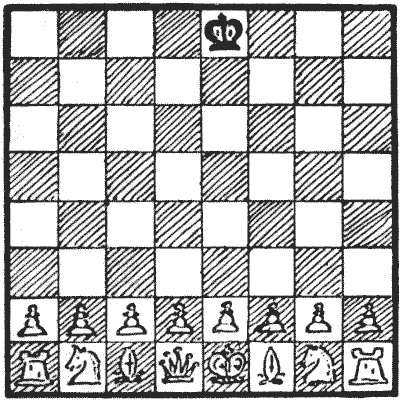  Set up the position shown in the diagram. Then the condition of the puzzle is—White to play and checkmate in six moves. Notwithstanding the complexities, I will show how the manner of play may be condensed into quite a few lines, merely stating here that the first two moves of White cannot be varied.
  Topics:

  Combinatorics -> Game Theory
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 350

• THE CRUSADER

  The following is a prize puzzle propounded by me some years ago. Produce a game of chess which, after sixteen moves, shall leave White with all his sixteen men on their original squares and Black in possession of his king alone (not necessarily on his own square). White is then to force mate in three moves.
  Topics:

  Combinatorics -> Game Theory Puzzles and Rebuses
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 351

• IMMOVABLE PAWNS

  Starting from the ordinary arrangement of the pieces as for a game, what is the smallest possible number of moves necessary in order to arrive at the following position? The moves for both sides must, of course, be played strictly in accordance with the rules of the game, though the result will necessarily be a very weird kind of chess.
  Topics:

  Combinatorics -> Game Theory
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 352

• ANCIENT CHINESE PUZZLE

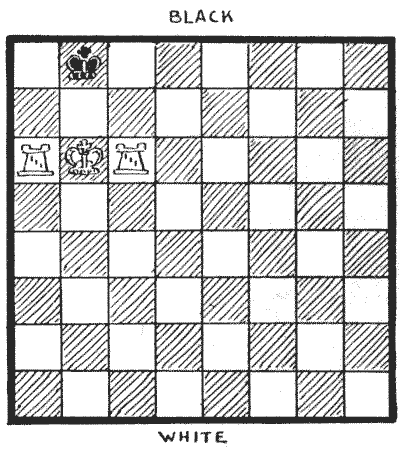  My next puzzle is supposed to be Chinese, many hundreds of years old, and never fails to interest. White to play and mate, moving each of the three pieces once, and once only.
  Topics:

  Combinatorics -> Game Theory Puzzles and Rebuses
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 357

• THE SIX PAWNS

  In how many different ways may I place six pawns on the chessboard so that there shall be an even number of unoccupied squares in every row and every column? We are not here considering the diagonals at all, and every different six squares occupied makes a different solution, so we have not to exclude reversals or reflections.
  Topics:

  Combinatorics -> Product Rule / Rule of Product
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 358