Combinatorics
Combinatorics is the art of counting. It deals with selections, arrangements, and combinations of objects. Questions involve determining the number of ways to perform tasks, arrange items (permutations), or choose subsets (combinations), often using principles like the product rule and sum rule.
Pigeonhole Principle Double Counting Binomial Coefficients and Pascal's Triangle Product Rule / Rule of Product Graph Theory Matchings Induction (Mathematical Induction) Game Theory Combinatorial Geometry Invariants Case Analysis / Checking Cases Processes / Procedures Number Tables Colorings-
DOMINOES IN PROGRESSION
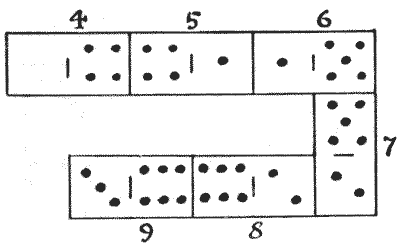 It will be seen that I have played six dominoes, in the illustration, in accordance with the ordinary rules of the game, `4` against `4, 1` against `1`, and so on, and yet the sum of the spots on the successive dominoes, `4, 5, 6, 7, 8, 9`, are in arithmetical progression; that is, the numbers taken in order have a common difference of `1`. In how many different ways may we play six dominoes, from an ordinary box of twenty-eight, so that the numbers on them may lie in arithmetical progression? We must always play from left to right, and numbers in decreasing arithmetical progression (such as `9, 8, 7, 6, 5, 4`) are not admissible.
Sources:Topics:Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures
It will be seen that I have played six dominoes, in the illustration, in accordance with the ordinary rules of the game, `4` against `4, 1` against `1`, and so on, and yet the sum of the spots on the successive dominoes, `4, 5, 6, 7, 8, 9`, are in arithmetical progression; that is, the numbers taken in order have a common difference of `1`. In how many different ways may we play six dominoes, from an ordinary box of twenty-eight, so that the numbers on them may lie in arithmetical progression? We must always play from left to right, and numbers in decreasing arithmetical progression (such as `9, 8, 7, 6, 5, 4`) are not admissible.
Sources:Topics:Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures- Amusements in Mathematics, Henry Ernest Dudeney Question 378
-
THE FIVE DOMINOES
Here is a new little puzzle that is not difficult, but will probably be found entertaining by my readers. It will be seen that the five dominoes are so arranged in proper sequence (that is, with `1` against `1, 2` against `2`, and so on), that the total number of pips on the two end dominoes is five, and the sum of the pips on the three dominoes in the middle is also five. There are just three other arrangements giving five for the additions. They are: —
(1—0) (0—0) (0—2) (2—1) (1—3) (4—0) (0—0) (0—2) (2—1) (1—0) (2—0) (0—0) (0—1) (1—3) (3—0) Now, how many similar arrangements are there of five dominoes that shall give six instead of five in the two additions?
Sources:- Amusements in Mathematics, Henry Ernest Dudeney Question 379
-
THE DOMINO FRAME PUZZLE
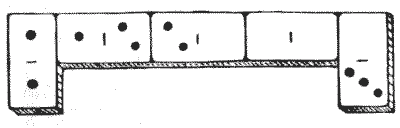
 It will be seen in the illustration that the full set of twenty-eight dominoes is arranged in the form of a square frame, with `6` against `6, 2` against `2`, blank against blank, and so on, as in the game. It will be found that the pips in the top row and left-hand column both add up `44`. The pips in the other two sides sum to `59` and `32` respectively. The puzzle is to rearrange the dominoes in the same form so that all of the four sides shall sum to `44`. Remember that the dominoes must be correctly placed one against another as in the game.
Sources:
It will be seen in the illustration that the full set of twenty-eight dominoes is arranged in the form of a square frame, with `6` against `6, 2` against `2`, blank against blank, and so on, as in the game. It will be found that the pips in the top row and left-hand column both add up `44`. The pips in the other two sides sum to `59` and `32` respectively. The puzzle is to rearrange the dominoes in the same form so that all of the four sides shall sum to `44`. Remember that the dominoes must be correctly placed one against another as in the game.
Sources:
- Amusements in Mathematics, Henry Ernest Dudeney Question 380
-
THE CARD FRAME PUZZLE
In the illustration we have a frame constructed from the ten playing cards, ace to ten of diamonds. The children who made it wanted the pips on all four sides to add up alike, but they failed in their attempt and gave it up as impossible. It will be seen that the pips in the top row, the bottom row, and the left-hand side all add up `14`, but the right-hand side sums to `23`. Now, what they were trying to do is quite possible. Can you rearrange the ten cards in the same formation so that all four sides shall add up alike? Of course they need not add up `14`, but any number you choose to select.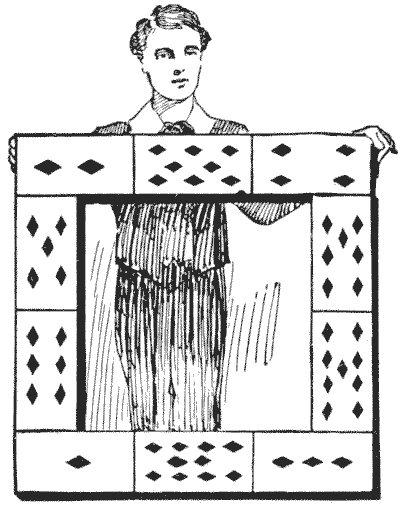 Sources:Topics:Arithmetic Algebra -> Equations Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures
Sources:Topics:Arithmetic Algebra -> Equations Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures- Amusements in Mathematics, Henry Ernest Dudeney Question 381
-
THE CROSS OF CARDS
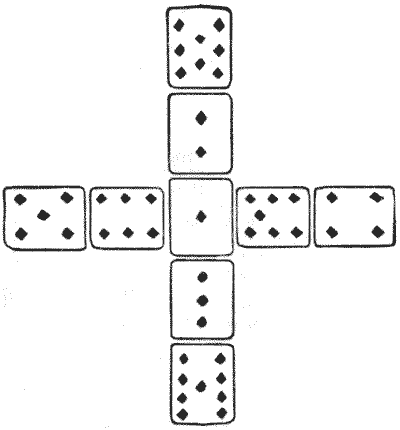 In this case we use only nine cards—the ace to nine of diamonds. The puzzle is to arrange them in the form of a cross, exactly in the way shown in the illustration, so that the pips in the vertical bar and in the horizontal bar add up alike. In the example given it will be found that both directions add up `23`. What I want to know is, how many different ways are there of rearranging the cards in order to bring about this result? It will be seen that, without affecting the solution, we may exchange the `5` with the `6`, the `5` with the `7`, the `8` with the `3`, and so on. Also we may make the horizontal and the vertical bars change places. But such obvious manipulations as these are not to be regarded as different solutions. They are all mere variations of one fundamental solution. Now, how many of these fundamentally different solutions are there? The pips need not, of course, always add up `23`.
Sources:
In this case we use only nine cards—the ace to nine of diamonds. The puzzle is to arrange them in the form of a cross, exactly in the way shown in the illustration, so that the pips in the vertical bar and in the horizontal bar add up alike. In the example given it will be found that both directions add up `23`. What I want to know is, how many different ways are there of rearranging the cards in order to bring about this result? It will be seen that, without affecting the solution, we may exchange the `5` with the `6`, the `5` with the `7`, the `8` with the `3`, and so on. Also we may make the horizontal and the vertical bars change places. But such obvious manipulations as these are not to be regarded as different solutions. They are all mere variations of one fundamental solution. Now, how many of these fundamentally different solutions are there? The pips need not, of course, always add up `23`.
Sources:
- Amusements in Mathematics, Henry Ernest Dudeney Question 382
-
THE "T" CARD PUZZLE
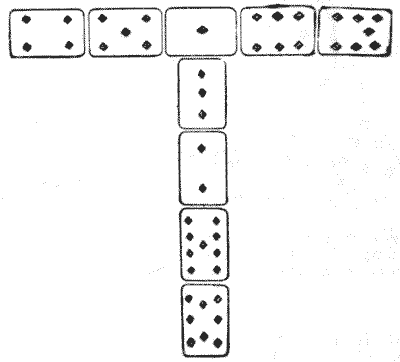 An entertaining little puzzle with cards is to take the nine cards of a suit, from ace to nine inclusive, and arrange them in the form of the letter "T," as shown in the illustration, so that the pips in the horizontal line shall count the same as those in the column. In the example given they add up twenty-three both ways. Now, it is quite easy to get a single correct arrangement. The puzzle is to discover in just how many different ways it may be done. Though the number is high, the solution is not really difficult if we attack the puzzle in the right manner. The reverse way obtained by reflecting the illustration in a mirror we will not count as different, but all other changes in the relative positions of the cards will here count. How many different ways are there?
Sources:Topics:Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Puzzles and Rebuses
An entertaining little puzzle with cards is to take the nine cards of a suit, from ace to nine inclusive, and arrange them in the form of the letter "T," as shown in the illustration, so that the pips in the horizontal line shall count the same as those in the column. In the example given they add up twenty-three both ways. Now, it is quite easy to get a single correct arrangement. The puzzle is to discover in just how many different ways it may be done. Though the number is high, the solution is not really difficult if we attack the puzzle in the right manner. The reverse way obtained by reflecting the illustration in a mirror we will not count as different, but all other changes in the relative positions of the cards will here count. How many different ways are there?
Sources:Topics:Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Puzzles and Rebuses- Amusements in Mathematics, Henry Ernest Dudeney Question 383
-
CARD TRIANGLES
Here you pick out the nine cards, ace to nine of diamonds, and arrange them in the form of a triangle, exactly as shown in the illustration, so that the pips add up the same on the three sides. In the example given it will be seen that they sum to `20` on each side, but the particular number is of no importance so long as it is the same on all three sides. The puzzle is to find out in just how many different ways this can be done.
If you simply turn the cards round so that one of the other two sides is nearest to you this will not count as different, for the order will be the same. Also, if you make the `4, 9, 5` change places with the `7, 3, 8`, and at the same time exchange the `1` and the `6`, it will not be different. But if you only change the `1` and the `6` it will be different, because the order round the triangle is not the same. This explanation will prevent any doubt arising as to the conditions.
Sources: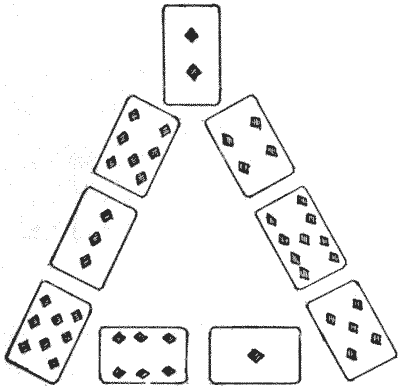
- Amusements in Mathematics, Henry Ernest Dudeney Question 384
-
"STRAND" PATIENCE
The idea for this came to me when considering the game of Patience that I gave in the Strand Magazine for December, `1910`, which has been reprinted in Ernest Bergholt's Second Book of Patience Games, under the new name of "King Albert."
Make two piles of cards as follows: `9` D, `8` S, `7` D, `6` S, `5` D, `4` S, `3` D, `2` S, `1` D, and `9` H, `8` C, `7` H, `6` C, `5` H, `4` C, `3` H, `2` C, `1` H, with the `9` of diamonds at the bottom of one pile and the `9` of hearts at the bottom of the other. The point is to exchange the spades with the clubs, so that the diamonds and clubs are still in numerical order in one pile and the hearts and spades in the other. There are four vacant spaces in addition to the two spaces occupied by the piles, and any card may be laid on a space, but a card can only be laid on another of the next higher value—an ace on a two, a two on a three, and so on. Patience is required to discover the shortest way of doing this. When there are four vacant spaces you can pile four cards in seven moves, with only three spaces you can pile them in nine moves, and with two spaces you cannot pile more than two cards. When you have a grasp of these and similar facts you will be able to remove a number of cards bodily and write down `7, 9`, or whatever the number of moves may be. The gradual shortening of play is fascinating, and first attempts are surprisingly lengthy.
Sources:Topics:Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Puzzles and Rebuses- Amusements in Mathematics, Henry Ernest Dudeney Question 385
-
THE FOOTBALL PLAYERS
"It is a glorious game!" an enthusiast was heard to exclaim. "At the close of last season, of the footballers of my acquaintance four had broken their left arm, five had broken their right arm, two had the right arm sound, and three had sound left arms." Can you discover from that statement what is the smallest number of players that the speaker could be acquainted with?
It does not at all follow that there were as many as fourteen men, because, for example, two of the men who had broken the left arm might also be the two who had sound right arms.
Sources:Topics:Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Minimum and Maximum Problems / Optimization Problems- Amusements in Mathematics, Henry Ernest Dudeney Question 389
-
THE PEBBLE GAME
Here is an interesting little puzzle game that I used to play with an acquaintance on the beach at Slocomb-on-Sea. Two players place an odd number of pebbles, we will say fifteen, between them. Then each takes in turn one, two, or three pebbles (as he chooses), and the winner is the one who gets the odd number. Thus, if you get seven and your opponent eight, you win. If you get six and he gets nine, he wins. Ought the first or second player to win, and how? When you have settled the question with fifteen pebbles try again with, say, thirteen.Sources:Topics:Combinatorics -> Game Theory Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures- Amusements in Mathematics, Henry Ernest Dudeney Question 392