Combinatorics, Combinatorial Geometry

Combinatorial Geometry explores the connections between combinatorics and geometry. It deals with problems about arrangements, configurations, and properties of discrete geometric objects (points, lines, polygons). Questions often involve counting, existence proofs, and geometric inequalities.

Cut a Shape / Dissection Problems Grid Paper Geometry / Lattice Geometry

  • THE YACHT RACE

    Now then, ye land-lubbers, hoist your baby-jib-topsails, break out your spinnakers, ease off your balloon sheets, and get your head-sails set!

    Our race consists in starting from the point at which the yacht is lying in the illustration and touching every one of the sixty-four buoys in fourteen straight courses, returning in the final tack to the buoy from which we start. The seventh course must finish at the buoy from which a flag is flying.

    This puzzle will call for a lot of skilful seamanship on account of the sharp angles at which it will occasionally be necessary to tack. The point of a lead pencil and a good nautical eye are all the outfit that we require.  

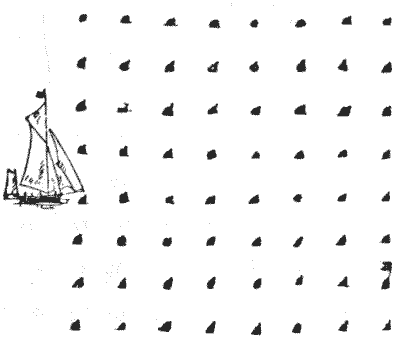
    This is difficult, because of the condition as to the flag-buoy, and because it is a re-entrant tour. But again we are allowed those oblique lines.

    Sources:

  • ST. GEORGE AND THE DRAGON

    Here is a little puzzle on a reduced chessboard of forty-nine squares. St. George wishes to kill the dragon. Killing dragons was a well-known pastime of his, and, being a knight, it was only natural that he should desire to perform the feat in a series of knight's moves. Can you show how, starting from that central square, he may visit once, and only once, every square of the board in a chain of chess knight's moves, and end by capturing the dragon on his last move? Of course a variety of different ways are open to him, so try to discover a route that forms some pretty design when you have marked each successive leap by a straight line from square to square. Sources:

  • FARMER LAWRENCE'S CORNFIELDS

    One of the most beautiful districts within easy distance of London for a summer ramble is that part of Buckinghamshire known as the Valley of the Chess—at least, it was a few years ago, before it was discovered by the speculative builder. At the beginning of the present century there lived, not far from Latimers, a worthy but eccentric farmer named Lawrence. One of his queer notions was that every person who lived near the banks of the river Chess ought to be in some way acquainted with the noble game of the same name, and in order to impress this fact on his men and his neighbours he adopted at times strange terminology. For example, when one of his ewes presented him with a lamb, he would say that it had "queened a pawn"; when he put up a new barn against the highway, he called it "castling on the king's side"; and when he sent a man with a gun to keep his neighbour's birds off his fields, he spoke of it as "attacking his opponent's rooks." Everybody in the neighbourhood used to be amused at Farmer Lawrence's little jokes, and one boy (the wag of the village) who got his ears pulled by the old gentleman for stealing his "chestnuts" went so far as to call him "a silly old chess-protector!"

    One year he had a large square field divided into forty-nine square plots, as shown in the illustration. The white squares were sown with wheat and the black squares with barley. When the harvest time came round he gave orders that his men were first to cut the corn in the patch marked `1`, and that each successive cutting should be exactly a knight's move from the last one, the thirteenth cutting being in the patch marked `13`, the twenty-fifth in the patch marked `25`, the thirty-seventh in the one marked `37`, and the last, or forty-ninth cutting, in the patch marked `49`. This was too much for poor Hodge, and each day Farmer Lawrence had to go down to the field and show which piece had to be operated upon. But the problem will perhaps present no difficulty to my readers.

    Sources:

  • THE FOUR KANGAROOS

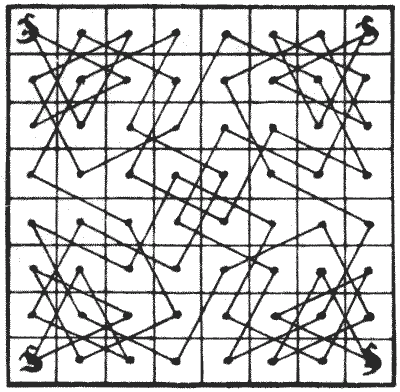    In introducing a little Commonwealth problem, I must first explain that the diagram represents the sixty-four fields, all properly fenced off from one another, of an Australian settlement, though I need hardly say that our kith and kin "down under" always do set out their land in this methodical and exact manner. It will be seen that in every one of the four corners is a kangaroo. Why kangaroos have a marked preference for corner plots has never been satisfactorily explained, and it would be out of place to discuss the point here. I should also add that kangaroos, as is well known, always leap in what we call "knight's moves." In fact, chess players would probably have adopted the better term "kangaroo's move" had not chess been invented before kangaroos.

    The puzzle is simply this. One morning each kangaroo went for his morning hop, and in sixteen consecutive knight's leaps visited just fifteen different fields and jumped back to his corner. No field was visited by more than one of the kangaroos. The diagram shows how they arranged matters. What you are asked to do is to show how they might have performed the feat without any kangaroo ever crossing the horizontal line in the middle of the square that divides the board into two equal parts.

    Sources:

  • THE MAGIC KNIGHT'S TOUR

    Here is a problem that has never yet been solved, nor has its impossibility been demonstrated. Play the knight once to every square of the chessboard in a complete tour, numbering the squares in the order visited, so that when completed the square shall be "magic," adding up to `260` in every column, every row, and each of the two long diagonals. I shall give the best answer that I have been able to obtain, in which there is a slight error in the diagonals alone. Can a perfect solution be found? I am convinced that it cannot, but it is only a "pious opinion."

    Sources: