Combinatorics, Combinatorial Geometry
Combinatorial Geometry explores the connections between combinatorics and geometry. It deals with problems about arrangements, configurations, and properties of discrete geometric objects (points, lines, polygons). Questions often involve counting, existence proofs, and geometric inequalities.
Cut a Shape / Dissection Problems Grid Paper Geometry / Lattice Geometry-
THE GRAND LAMA'S PROBLEM
Once upon a time there was a Grand Lama who had a chessboard made of pure gold, magnificently engraved, and, of course, of great value. Every year a tournament was held at Lhassa among the priests, and whenever any one beat the Grand Lama it was considered a great honour, and his name was inscribed on the back of the board, and a costly jewel set in the particular square on which the checkmate had been given. After this sovereign pontiff had been defeated on four occasions he died—possibly of chagrin.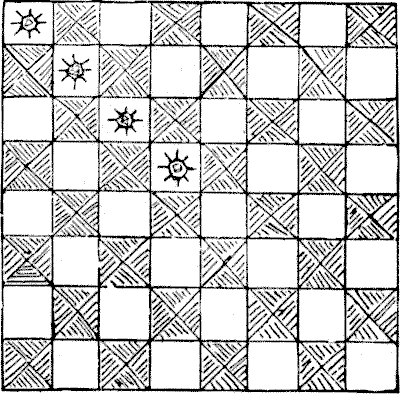
Now the new Grand Lama was an inferior chess-player, and preferred other forms of innocent amusement, such as cutting off people's heads. So he discouraged chess as a degrading game, that did not improve either the mind or the morals, and abolished the tournament summarily. Then he sent for the four priests who had had the effrontery to play better than a Grand Lama, and addressed them as follows: "Miserable and heathenish men, calling yourselves priests! Know ye not that to lay claim to a capacity to do anything better than my predecessor is a capital offence? Take that chessboard and, before day dawns upon the torture chamber, cut it into four equal parts of the same shape, each containing sixteen perfect squares, with one of the gems in each part! If in this you fail, then shall other sports be devised for your special delectation. Go!" The four priests succeeded in their apparently hopeless task. Can you show how the board may be divided into four equal parts, each of exactly the same shape, by cuts along the lines dividing the squares, each part to contain one of the gems?
Sources:Topics:Combinatorics -> Colorings -> Chessboard Coloring Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Puzzles and Rebuses- Amusements in Mathematics, Henry Ernest Dudeney Question 291
-
THE CHESSBOARD SENTENCE
I once set myself the amusing task of so dissecting an ordinary chessboard into letters of the alphabet that they would form a complete sentence. It will be seen from the illustration that the pieces assembled give the sentence, "CUT THY LIFE," with the stops between. The ideal sentence would, of course, have only one full stop, but that I did not succeed in obtaining.
The sentence is an appeal to the transgressor to cut himself adrift from the evil life he is living. Can you fit these pieces together to form a perfect chessboard?
Sources:Topics:Combinatorics -> Colorings -> Chessboard Coloring Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Puzzles and Rebuses- Amusements in Mathematics, Henry Ernest Dudeney Question 294
-
A CHESSBOARD FALLACY
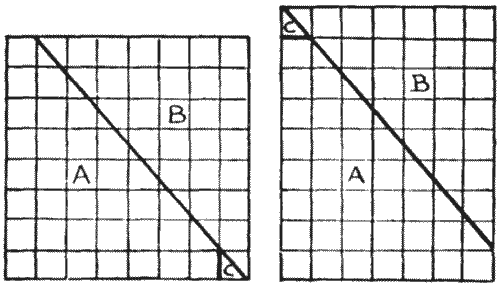
"Here is a diagram of a chessboard," he said. "You see there are sixty-four squares—eight by eight. Now I draw a straight line from the top left-hand corner, where the first and second squares meet, to the bottom right-hand corner. I cut along this line with the scissors, slide up the piece that I have marked B, and then clip off the little corner C by a cut along the first upright line. This little piece will exactly fit into its place at the top, and we now have an oblong with seven squares on one side and nine squares on the other. There are, therefore, now only sixty-three squares, because seven multiplied by nine makes sixty-three. Where on earth does that lost square go to? I have tried over and over again to catch the little beggar, but he always eludes me. For the life of me I cannot discover where he hides himself."
"It seems to be like the other old chessboard fallacy, and perhaps the explanation is the same," said Reginald—"that the pieces do not exactly fit."
"But they do fit," said Uncle John. "Try it, and you will see."
Later in the evening Reginald and George, were seen in a corner with their heads together, trying to catch that elusive little square, and it is only fair to record that before they retired for the night they succeeded in securing their prey, though some others of the company failed to see it when captured. Can the reader solve the little mystery?
Sources:Topics:Geometry -> Plane Geometry Geometry -> Area Calculation Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems- Amusements in Mathematics, Henry Ernest Dudeney Question 413
-
Question
On an infinite grid of squares, 6 squares are marked, as in the diagram. How many squares contain stones? In one move, a stone can be removed if it has no adjacent stone above and to its right; then, two stones are placed in the squares above and to the right of the removed stone. Can we remove all stones from the marked squares if the initial state is:
A. (8 points) All marked squares.
B. (8 points) Only the bottom-left marked square.O
O O
O O OM. Konvitz'
Sources: -
Question
What is the maximum number of chess kings that can be placed on an `8xx8` board such that they do not threaten each other?
Topics:Combinatorics -> Pigeonhole Principle Proof and Example -> Constructing an Example / Counterexample Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Minimum and Maximum Problems / Optimization Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry -
The Beaver and the Mole
There is a plot of land in the shape of a square `4 times 4` divided into cells of `1 times 1`. The beaver wants to build a house on it that occupies 4 cells, which from a top-down view looks like this:
The mole wants to disturb him. For this purpose, it can dig holes, each of which occupies one cell. It is impossible to build on the cells that have become holes. What is the smallest number of holes the mole needs to dig so that the beaver cannot build the house?
Sources: -
Orange Star of David
The area of the blue triangle is equal to 1. Calculate the area of the orange Star of David:
Sources:
-
Two Hashes
What is the maximum number of "domino" shapes (rectangles `1 times 2` or `2 times 1`) that can be placed inside the orange shape,
such that they do not overlap and do not extend beyond the boundaries of the shape?
Sources:
-
Largest Perimeter
A polygon with an area of 12 is drawn on grid paper, with all its sides passing through the grid lines. What is the largest possible perimeter of this polygon?
Sources: -
Drawing of a Relation
Given a 5x5 grid divided into 1x1 squares. Two squares are considered related if they are in the same row or column, and the distance between their centers is 2 or 3.
For example, in the drawing, all the squares related to the red square are marked in gray. Sammy receives a blank grid and wants to mark as many squares as possible such that no two of them are related. What is the maximum number of squares he can mark?
Sources:Topics:Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Minimum and Maximum Problems / Optimization Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry- Gillis Mathematical Olympiad, 2018-2019 Question 2