Combinatorics, Combinatorial Geometry

Combinatorial Geometry explores the connections between combinatorics and geometry. It deals with problems about arrangements, configurations, and properties of discrete geometric objects (points, lines, polygons). Questions often involve counting, existence proofs, and geometric inequalities.

• Question

  Cut the given shape into "T" shapes as shown in the diagram:

  

  Topics:

  Geometry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry

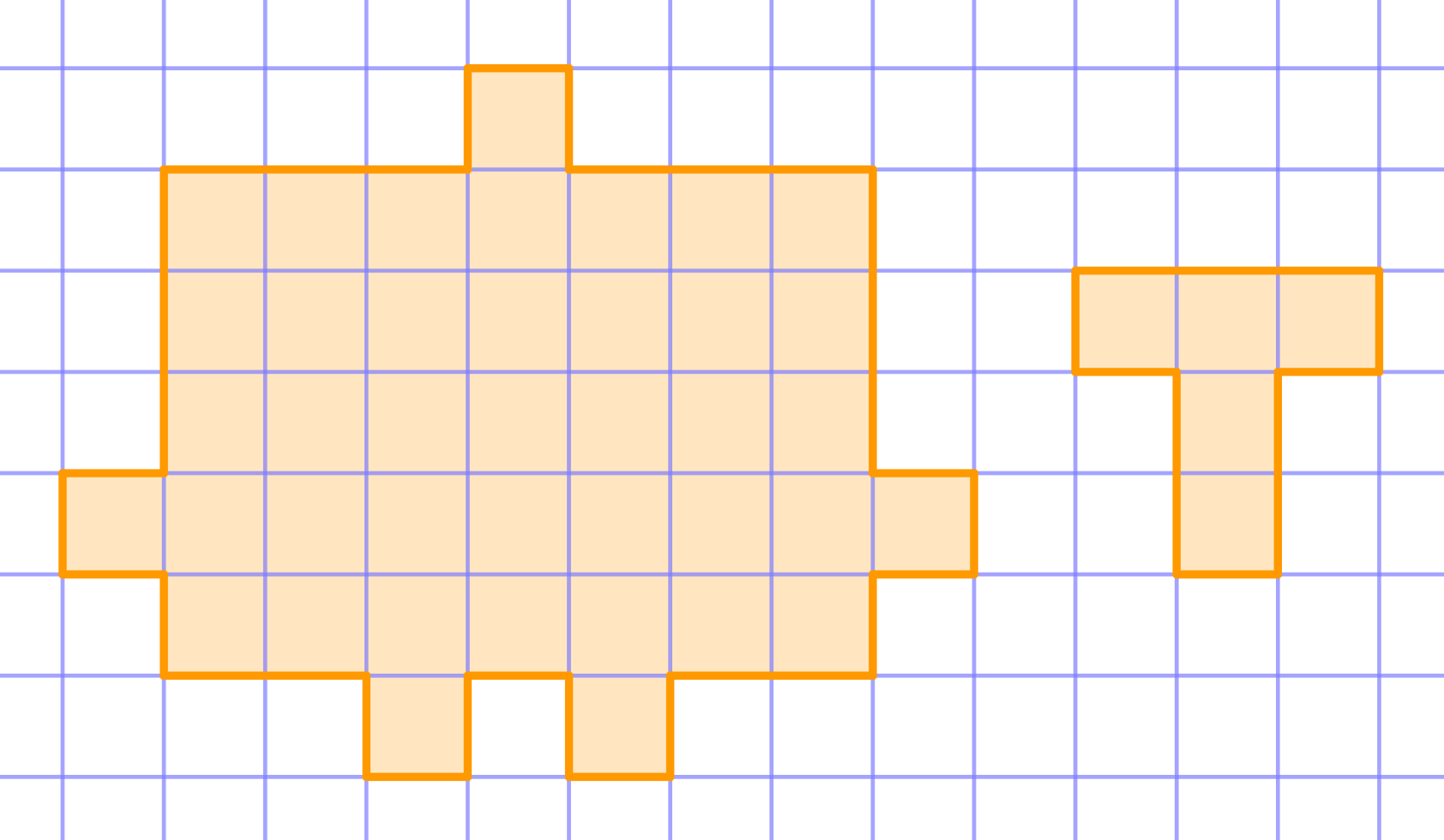
• Question

  Is there a quadrilateral that can be cut into `6` parts by two straight cuts? Justify your answer or provide an example.

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Plane Geometry Proof and Example -> Constructing an Example / Counterexample Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems

• Question

  It is known that all the angles of the given shape are right angles. Cut the shape into two polygons of equal area. You are only allowed to use an unmarked ruler.

  

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Symmetry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems

• Question

  Prove that the given shape cannot be cut into dominoes:

  

  Topics:

  Combinatorics -> Invariants Combinatorics -> Matchings Number Theory -> Division -> Parity (Even/Odd) Proof and Example -> Proof by Contradiction Combinatorics -> Colorings -> Chessboard Coloring Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems

• Question

  Can you cut the shape on the left into six shapes like the shape on the right?

  

  Topics:

  Combinatorics -> Invariants Combinatorics -> Matchings Proof and Example Combinatorics -> Colorings -> Chessboard Coloring Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry

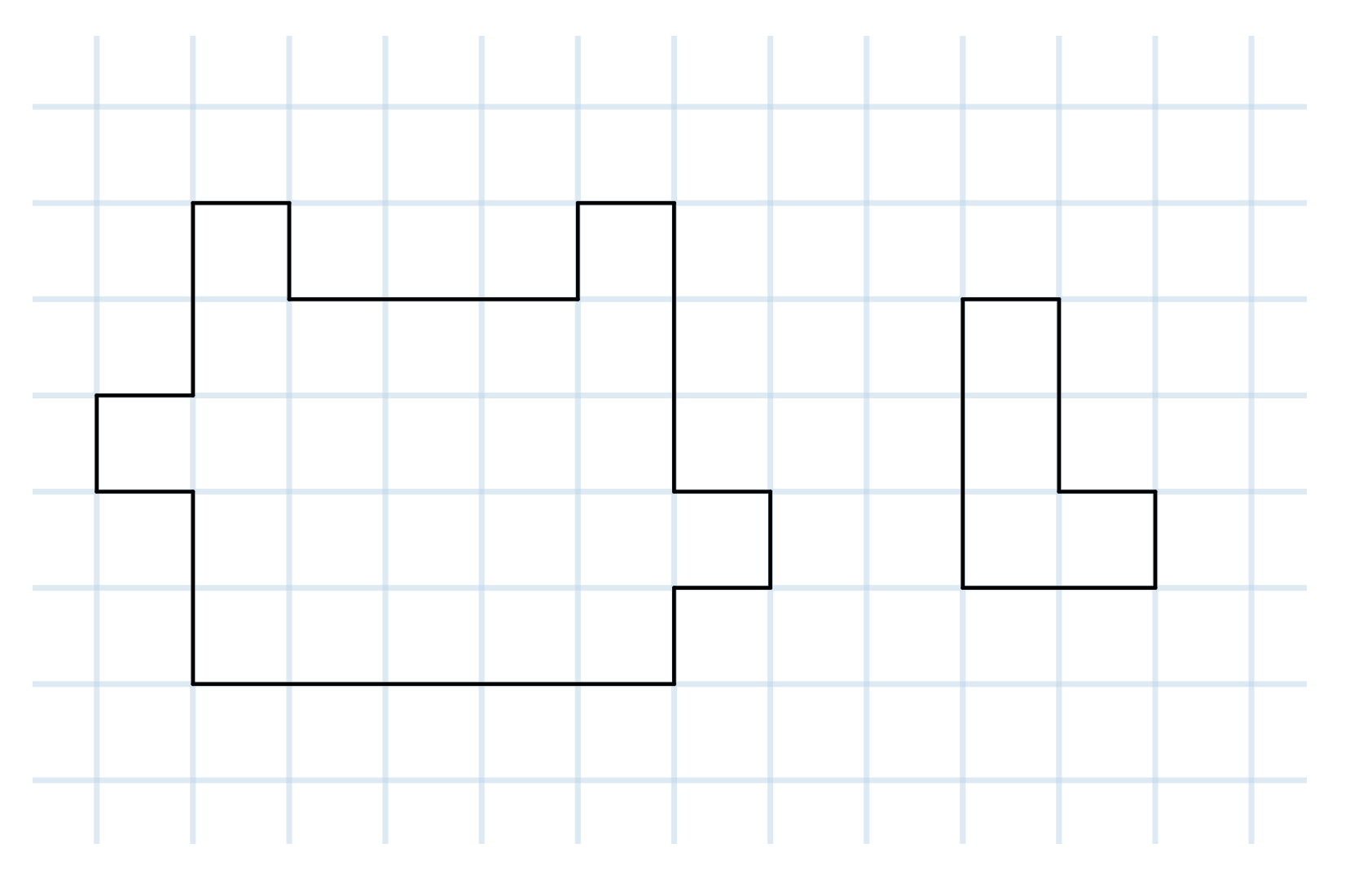
• Area of the Shape

  Given a grid paper where the area of each square is one unit area. Find the area of the shape (in unit areas)

   

  

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Plane Geometry Geometry -> Area Calculation Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry
  Sources:
  • Young Mathematician Olympiad, 2017-2018, Stage A, Grades 3-4 Question 7

• Cutting

  What is the largest number of rectangles of size `2 times 5`  that can be cut from a `9 times 9` square?

  Topics:

  Geometry -> Area Calculation Proof and Example -> Constructing an Example / Counterexample Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry
  Sources:
  • Young Mathematician Olympiad, 2018-2019, Stage A, Grades 3-4 Question 1
  • Young Mathematician Olympiad, 2018-2019, Stage A, Grades 5-6 Question 1

• Squares

  You have many cardboard squares of sizes `1 times 1`, `2 times 2`, and `3 times 3`, and you must assemble them into a square of size `7 times 7`.
  What is the smallest possible number of squares you will need?

  Topics:

  Geometry Minimum and Maximum Problems / Optimization Problems Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems
  Sources:
  • Young Mathematician Olympiad, 2018-2019, Stage B, Grades 3-4 Question 5

• Dissect into four parts

  Geometric shapes are called congruent if they coincide when superimposed. Cut the following shape into four congruent parts:

  

  Topics:

  Geometry -> Plane Geometry -> Symmetry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries)
  Sources:
  • Young Mathematician Olympiad, 2019-2020, Final, Grades 3-4 Question 3

• Cut a Boat in Half

  Geometric shapes are called congruent if they coincide when placed on top of each other. Cut the shape into two congruent parts

  

  Topics:

  Geometry -> Plane Geometry -> Symmetry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems
  Sources:
  • Young Mathematician Olympiad, 2019-2020, Final, Grades 5-6 Question 6