Combinatorics, Combinatorial Geometry
Combinatorial Geometry explores the connections between combinatorics and geometry. It deals with problems about arrangements, configurations, and properties of discrete geometric objects (points, lines, polygons). Questions often involve counting, existence proofs, and geometric inequalities.
Cut a Shape / Dissection Problems Grid Paper Geometry / Lattice Geometry-
Knight's Moves
A knight moves on an infinite grid. It starts at the point (0,0) and must reach
the point (5,27). Assuming it moves in the smallest number of steps required,
how many different possibilities does it have to reach this point?Sources: -
It's Crowded Here!
55 gears are placed on the game board in the shape of a 'pyramid':
10 gears in the bottom row, 9 gears in the row above, and so on.
In this state, the gears cannot rotate freely (convince yourself why!)
Remove gears to allow free movement.
What is the maximum number of gears that can remain on the board so that they can all rotate?
Sources:Topics:Proof and Example -> Constructing an Example / Counterexample Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry- Bar-Ilan's weekly mathriddle competition, 2024 Question 10
-
A PLANTATION PUZZLE
 A man had a square plantation of forty-nine trees, but, as will be seen by the omissions in the illustration, four trees were blown down and removed. He now wants to cut down all the remainder except ten trees, which are to be so left that they shall form five straight rows with four trees in every row. Which are the ten trees that he must leave?
Sources:
A man had a square plantation of forty-nine trees, but, as will be seen by the omissions in the illustration, four trees were blown down and removed. He now wants to cut down all the remainder except ten trees, which are to be so left that they shall form five straight rows with four trees in every row. Which are the ten trees that he must leave?
Sources:
- Amusements in Mathematics, Henry Ernest Dudeney Question 208
-
TORPEDO PRACTICE
 If a fleet of sixteen men-of-war were lying at anchor and surrounded by the enemy, how many ships might be sunk if every torpedo, projected in a straight line, passed under three vessels and sank the fourth? In the diagram we have arranged the fleet in square formation, where it will be seen that as many as seven ships may be sunk (those in the top row and first column) by firing the torpedoes indicated by arrows. Anchoring the fleet as we like, to what extent can we increase this number? Remember that each successive ship is sunk before another torpedo is launched, and that every torpedo proceeds in a different direction; otherwise, by placing the ships in a straight line, we might sink as many as thirteen! It is an interesting little study in naval warfare, and eminently practical—provided the enemy will allow you to arrange his fleet for your convenience and promise to lie still and do nothing!
Sources:
If a fleet of sixteen men-of-war were lying at anchor and surrounded by the enemy, how many ships might be sunk if every torpedo, projected in a straight line, passed under three vessels and sank the fourth? In the diagram we have arranged the fleet in square formation, where it will be seen that as many as seven ships may be sunk (those in the top row and first column) by firing the torpedoes indicated by arrows. Anchoring the fleet as we like, to what extent can we increase this number? Remember that each successive ship is sunk before another torpedo is launched, and that every torpedo proceeds in a different direction; otherwise, by placing the ships in a straight line, we might sink as many as thirteen! It is an interesting little study in naval warfare, and eminently practical—provided the enemy will allow you to arrange his fleet for your convenience and promise to lie still and do nothing!
Sources:
- Amusements in Mathematics, Henry Ernest Dudeney Question 235
-
THE CROSS TARGET
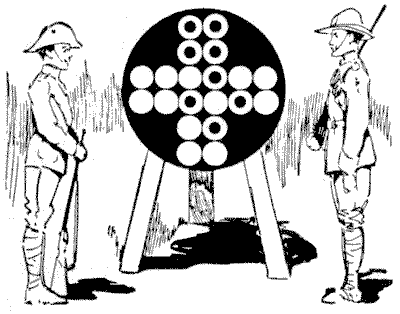 In the illustration we have a somewhat curious target designed by an eccentric sharpshooter. His idea was that in order to score you must hit four circles in as many shots so that those four shots shall form a square. It will be seen by the results recorded on the target that two attempts have been successful. The first man hit the four circles at the top of the cross, and thus formed his square. The second man intended to hit the four in the bottom arm, but his second shot, on the left, went too high. This compelled him to complete his four in a different way than he intended. It will thus be seen that though it is immaterial which circle you hit at the first shot, the second shot may commit you to a definite procedure if you are to get your square. Now, the puzzle is to say in just how many different ways it is possible to form a square on the target with four shots.
Sources:Topics:Geometry Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry
In the illustration we have a somewhat curious target designed by an eccentric sharpshooter. His idea was that in order to score you must hit four circles in as many shots so that those four shots shall form a square. It will be seen by the results recorded on the target that two attempts have been successful. The first man hit the four circles at the top of the cross, and thus formed his square. The second man intended to hit the four in the bottom arm, but his second shot, on the left, went too high. This compelled him to complete his four in a different way than he intended. It will thus be seen that though it is immaterial which circle you hit at the first shot, the second shot may commit you to a definite procedure if you are to get your square. Now, the puzzle is to say in just how many different ways it is possible to form a square on the target with four shots.
Sources:Topics:Geometry Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry- Amusements in Mathematics, Henry Ernest Dudeney Question 284
-
THE FIVE CRESCENTS OF BYZANTIUM
When Philip of Macedon, the father of Alexander the Great, found himself confronted with great difficulties in the siege of Byzantium, he set his men to undermine the walls. His desires, however, miscarried, for no sooner had the operations been begun than a crescent moon suddenly appeared in the heavens and discovered his plans to his adversaries. The Byzantines were naturally elated, and in order to show their gratitude they erected a statue to Diana, and the crescent became thenceforward a symbol of the state. In the temple that contained the statue was a square pavement composed of sixty-four large and costly tiles. These were all plain, with the exception of five, which bore the symbol of the crescent. These five were for occult reasons so placed that every tile should be watched over by (that is, in a straight line, vertically, horizontally, or diagonally with) at least one of the crescents. The arrangement adopted by the Byzantine architect was as follows:—

Now, to cover up one of these five crescents was a capital offence, the death being something very painful and lingering. But on a certain occasion of festivity it was necessary to lay down on this pavement a square carpet of the largest dimensions possible, and I have shown in the illustration by dark shading the largest dimensions that would be available.
The puzzle is to show how the architect, if he had foreseen this question of the carpet, might have so arranged his five crescent tiles in accordance with the required conditions, and yet have allowed for the largest possible square carpet to be laid down without any one of the five crescent tiles being covered, or any portion of them.
Sources:Topics:Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry Puzzles and Rebuses- Amusements in Mathematics, Henry Ernest Dudeney Question 312
-
THE SOUTHERN CROSS

In the above illustration we have five Planets and eighty-one Fixed Stars, five of the latter being hidden by the Planets. It will be found that every Star, with the exception of the ten that have a black spot in their centres, is in a straight line, vertically, horizontally, or diagonally, with at least one of the Planets. The puzzle is so to rearrange the Planets that all the Stars shall be in line with one or more of them.
In rearranging the Planets, each of the five may be moved once in a straight line, in either of the three directions mentioned. They will, of course, obscure five other Stars in place of those at present covered.
Sources:Topics:Logic -> Reasoning / Logic Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry Puzzles and Rebuses- Amusements in Mathematics, Henry Ernest Dudeney Question 314
-
A PUZZLE WITH PAWNS
Place two pawns in the middle of the chessboard, one at Q `4` and the other at K `5`. Now, place the remaining fourteen pawns (sixteen in all) so that no three shall be in a straight line in any possible direction.
Note that I purposely do not say queens, because by the words "any possible direction" I go beyond attacks on diagonals. The pawns must be regarded as mere points in space—at the centres of the squares. See dotted lines in the case of No. `300`, "The Eight Queens."
Sources:- Amusements in Mathematics, Henry Ernest Dudeney Question 317
-
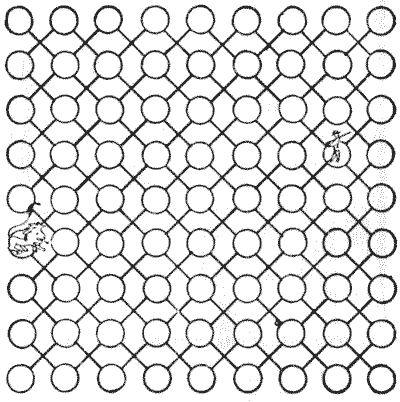
LION-HUNTING
My friend Captain Potham Hall, the renowned hunter of big game, says there is nothing more exhilarating than a brush with a herd—a pack—a team—a flock—a swarm (it has taken me a full quarter of an hour to recall the right word, but I have it at last)—a pride of lions. Why a number of lions are called a "pride," a number of whales a "school," and a number of foxes a "skulk" are mysteries of philology into which I will not enter.
Well, the captain says that if a spirited lion crosses your path in the desert it becomes lively, for the lion has generally been looking for the man just as much as the man has sought the king of the forest. And yet when they meet they always quarrel and fight it out. A little contemplation of this unfortunate and long-standing feud between two estimable families has led me to figure out a few calculations as to the probability of the man and the lion crossing one another's path in the jungle. In all these cases one has to start on certain more or less arbitrary assumptions. That is why in the above illustration I have thought it necessary to represent the paths in the desert with such rigid regularity. Though the captain assures me that the tracks of the lions usually run much in this way, I have doubts.
The puzzle is simply to find out in how many different ways the man and the lion may be placed on two different spots that are not on the same path. By "paths" it must be understood that I only refer to the ruled lines. Thus, with the exception of the four corner spots, each combatant is always on two paths and no more. It will be seen that there is a lot of scope for evading one another in the desert, which is just what one has always understood.
Sources:Topics:Combinatorics -> Product Rule / Rule of Product Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry- Amusements in Mathematics, Henry Ernest Dudeney Question 318
-
THE ROOK'S JOURNEY
This puzzle I call "The Rook's Journey," because the word "tour" (derived from a turner's wheel) implies that we return to the point from which we set out, and we do not do this in the present case. We should not be satisfied with a personally conducted holiday tour that ended by leaving us, say, in the middle of the Sahara. The rook here makes twenty-one moves, in the course of which journey it visits every square of the board once and only once, stopping at the square marked `10` at the end of its tenth move, and ending at the square marked `21`. Two consecutive moves cannot be made in the same direction—that is to say, you must make a turn after every move.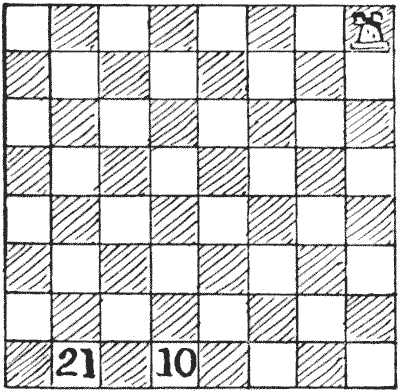 Sources:Topics:Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry Puzzles and Rebuses
Sources:Topics:Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry Puzzles and Rebuses- Amusements in Mathematics, Henry Ernest Dudeney Question 321
