Algebra, Equations
An equation is a statement that two mathematical expressions are equal. Solving an equation involves finding the values of variables that make the statement true. Questions cover various types: linear, quadratic, polynomial, rational, radical, and systems of equations.
Diophantine Equations-
THE CRESCENT PUZZLE
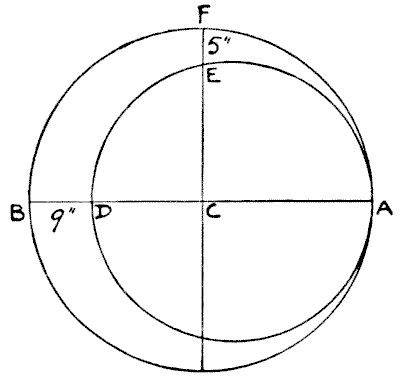 Here is an easy geometrical puzzle. The crescent is formed by two circles, and C is the centre of the larger circle. The width of the crescent between B and D is `9` inches, and between E and F `5` inches. What are the diameters of the two circles?
Sources:
Here is an easy geometrical puzzle. The crescent is formed by two circles, and C is the centre of the larger circle. The width of the crescent between B and D is `9` inches, and between E and F `5` inches. What are the diameters of the two circles?
Sources:
- Amusements in Mathematics, Henry Ernest Dudeney Question 191
-
LADY BELINDA'S GARDEN
Lady Belinda is an enthusiastic gardener. In the illustration she is depicted in the act of worrying out a pleasant little problem which I will relate. One of her gardens is oblong in shape, enclosed by a high holly hedge, and she is turning it into a rosary for the cultivation of some of her choicest roses. She wants to devote exactly half of the area of the garden to the flowers, in one large bed, and the other half to be a path going all round it of equal breadth throughout. Such a garden is shown in the diagram at the foot of the picture. How is she to mark out the garden under these simple conditions? She has only a tape, the length of the garden, to do it with, and, as the holly hedge is so thick and dense, she must make all her measurements inside. Lady Belinda did not know the exact dimensions of the garden, and, as it was not necessary for her to know, I also give no dimensions. It is quite a simple task no matter what the size or proportions of the garden may be. Yet how many lady gardeners would know just how to proceed? The tape may be quite plain—that is, it need not be a graduated measure. Sources:Topics:Geometry -> Plane Geometry Geometry -> Area Calculation Algebra -> Algebraic Techniques Algebra -> Equations
Sources:Topics:Geometry -> Plane Geometry Geometry -> Area Calculation Algebra -> Algebraic Techniques Algebra -> Equations- Amusements in Mathematics, Henry Ernest Dudeney Question 195
-
THE KEG OF WINE
Here is a curious little problem. A man had a ten-gallon keg full of wine and a jug. One day he drew off a jugful of wine and filled up the keg with water. Later on, when the wine and water had got thoroughly mixed, he drew off another jugful and again filled up the keg with water. It was then found that the keg contained equal proportions of wine and water. Can you find from these facts the capacity of the jug? Sources:- Amusements in Mathematics, Henry Ernest Dudeney Question 368
-
MIXING THE TEA
"Mrs. Spooner called this morning," said the honest grocer to his assistant. "She wants twenty pounds of tea at `2`s. `4`½d. per lb. Of course we have a good `2`s. `6`d. tea, a slightly inferior at `2`s. `3`d., and a cheap Indian at `1`s. `9`d., but she is very particular always about her prices."
"What do you propose to do?" asked the innocent assistant.
"Do?" exclaimed the grocer. "Why, just mix up the three teas in different proportions so that the twenty pounds will work out fairly at the lady's price. Only don't put in more of the best tea than you can help, as we make less profit on that, and of course you will use only our complete pound packets. Don't do any weighing."
How was the poor fellow to mix the three teas? Could you have shown him how to do it?
Sources:- Amusements in Mathematics, Henry Ernest Dudeney Question 369
-
THE CARD FRAME PUZZLE
In the illustration we have a frame constructed from the ten playing cards, ace to ten of diamonds. The children who made it wanted the pips on all four sides to add up alike, but they failed in their attempt and gave it up as impossible. It will be seen that the pips in the top row, the bottom row, and the left-hand side all add up `14`, but the right-hand side sums to `23`. Now, what they were trying to do is quite possible. Can you rearrange the ten cards in the same formation so that all four sides shall add up alike? Of course they need not add up `14`, but any number you choose to select.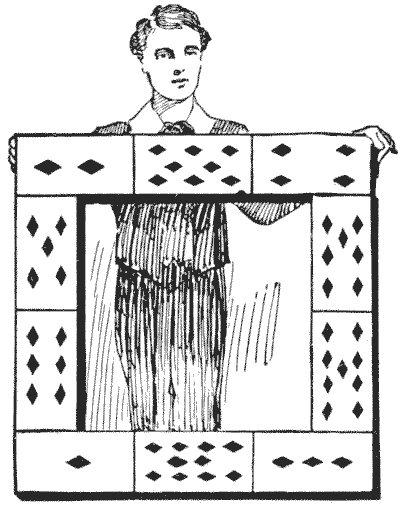 Sources:Topics:Arithmetic Algebra -> Equations Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures
Sources:Topics:Arithmetic Algebra -> Equations Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures- Amusements in Mathematics, Henry Ernest Dudeney Question 381
-
THE HORSE-RACE PUZZLE
There are no morals in puzzles. When we are solving the old puzzle of the captain who, having to throw half his crew overboard in a storm, arranged to draw lots, but so placed the men that only the Turks were sacrificed, and all the Christians left on board, we do not stop to discuss the questionable morality of the proceeding. And when we are dealing with a measuring problem, in which certain thirsty pilgrims are to make an equitable division of a barrel of beer, we do not object that, as total abstainers, it is against our conscience to have anything to do with intoxicating liquor. Therefore I make no apology for introducing a puzzle that deals with betting.
Three horses—Acorn, Bluebottle, and Capsule—start in a race. The odds are `4` to `1`, Acorn; `3` to `1`, Bluebottle; `2` to `1`, Capsule. Now, how much must I invest on each horse in order to win £`13`, no matter which horse comes in first? Supposing, as an example, that I betted £`5` on each horse. Then, if Acorn won, I should receive £`20` (four times £`5`), and have to pay £`5` each for the other two horses; thereby winning £`10`. But it will be found that if Bluebottle was first I should only win £`5`, and if Capsule won I should gain nothing and lose nothing. This will make the question perfectly clear to the novice, who, like myself, is not interested in the calling of the fraternity who profess to be engaged in the noble task of "improving the breed of horses."
Sources:- Amusements in Mathematics, Henry Ernest Dudeney Question 390
-
THE MOTOR-CAR RACE
Sometimes a quite simple statement of fact, if worded in an unfamiliar manner, will cause considerable perplexity. Here is an example, and it will doubtless puzzle some of my more youthful readers just a little. I happened to be at a motor-car race at Brooklands, when one spectator said to another, while a number of cars were whirling round and round the circular track:—
"There's Gogglesmith—that man in the white car!"
"Yes, I see," was the reply; "but how many cars are running in this race?"
Then came this curious rejoinder:—
"One-third of the cars in front of Gogglesmith added to three-quarters of those behind him will give you the answer."
Now, can you tell how many cars were running in the race?
Sources:- Amusements in Mathematics, Henry Ernest Dudeney Question 391
-
Question
Find all integer solutions `(k>1) y^k=x^2+x`
Sources:Topics:Number Theory -> Prime Numbers -> Prime Factorization Number Theory -> Greatest Common Divisor (GCD) and Least Common Multiple (LCM) Algebra -> Equations -> Diophantine Equations- Tournament of Towns, 1980-1981, Spring, Main Version, Grades 9-10 Question 1 Points 3
-
Question
Find a two-digit number that is twice as large as the product of its digits.
Sources: -
Question
There are chairs with `4` legs and with `3` legs in a room. When people sat on all the chairs, there were `39` legs in the room (no one remained standing). How many chairs of each type are there in the room?