Algebra, Equations

An equation is a statement that two mathematical expressions are equal. Solving an equation involves finding the values of variables that make the statement true. Questions cover various types: linear, quadratic, polynomial, rational, radical, and systems of equations.

Diophantine Equations

  • THE FOUR SEVENS

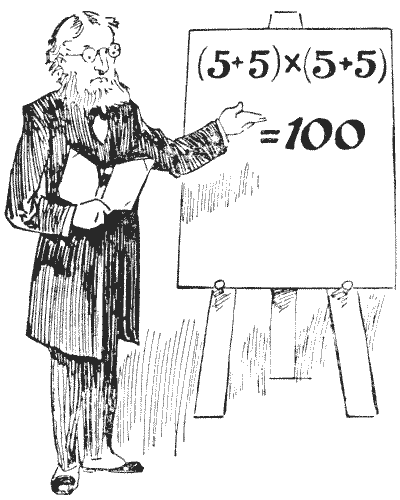    In the illustration Professor Rackbrane is seen demonstrating one of the little posers with which he is accustomed to entertain his class. He believes that by taking his pupils off the beaten tracks he is the better able to secure their attention, and to induce original and ingenious methods of thought. He has, it will be seen, just shown how four `5`'s may be written with simple arithmetical signs so as to represent `100`. Every juvenile reader will see at a glance that his example is quite correct. Now, what he wants you to do is this: Arrange four `7`'s (neither more nor less) with arithmetical signs so that they shall represent `100`. If he had said we were to use four `9`'s we might at once have written `99 9/9`, but the four `7`'s call for rather more ingenuity. Can you discover the little trick?

    Sources:

  • THE SPOT ON THE TABLE

    A boy, recently home from school, wished to give his father an exhibition of his precocity. He pushed a large circular table into the corner of the room, as shown in the illustration, so that it touched both walls, and he then pointed to a spot of ink on the extreme edge.

     

    "Here is a little puzzle for you, pater," said the youth. "That spot is exactly eight inches from one wall and nine inches from the other. Can you tell me the diameter of the table without measuring it?"

    The boy was overheard to tell a friend, "It fairly beat the guv'nor;" but his father is known to have remarked to a City acquaintance that he solved the thing in his head in a minute. I often wonder which spoke the truth.

    Sources:

  • ACADEMIC COURTESIES

    In a certain mixed school, where a special feature was made of the inculcation of good manners, they had a curious rule on assembling every morning. There were twice as many girls as boys. Every girl made a bow to every other girl, to every boy, and to the teacher. Every boy made a bow to every other boy, to every girl, and to the teacher. In all there were nine hundred bows made in that model academy every morning. Now, can you say exactly how many boys there were in the school? If you are not very careful, you are likely to get a good deal out in your calculation. Sources:

  • THE THIRTY-THREE PEARLS

    "A man I know," said Teddy Nicholson at a certain family party, "possesses a string of thirty-three pearls. The middle pearl is the largest and best of all, and the others are so selected and arranged that, starting from one end, each successive pearl is worth £`100` more than the preceding one, right up to the big pearl. From the other end the pearls increase in value by £`150` up to the large pearl. The whole string is worth £`65,000`. What is the value of that large pearl?"

     

    "Pearls and other articles of clothing," said Uncle Walter, when the price of the precious gem had been discovered, "remind me of Adam and Eve. Authorities, you may not know, differ as to the number of apples that were eaten by Adam and Eve. It is the opinion of some that Eve `8` (ate) and Adam `2` (too), a total of `10` only. But certain mathematicians have figured it out differently, and hold that Eve `8` and Adam a total of `16`. Yet the most recent investigators think the above figures entirely wrong, for if Eve `8` and Adam `82`, the total must be `90`."

    "Well," said Harry, "it seems to me that if there were giants in those days, probably Eve `81` and Adam `82`, which would give a total of `163`."

    "I am not at all satisfied," said Maud. "It seems to me that if Eve `81` and Adam `812`, they together consumed `893`."

    "I am sure you are all wrong," insisted Mr. Wilson, "for I consider that Eve `814` Adam, and Adam `8124` Eve, so we get a total of `8,938`."

    "But, look here," broke in Herbert. "If Eve `814` Adam and Adam `81242` oblige Eve, surely the total must have been `82,056`!"

    At this point Uncle Walter suggested that they might let the matter rest. He declared it to be clearly what mathematicians call an indeterminate problem.

    Sources:

  • THE LABOURER'S PUZZLE

    Professor Rackbrane, during one of his rambles, chanced to come upon a man digging a deep hole.

    "Good morning," he said. "How deep is that hole?"

    "Guess," replied the labourer. "My height is exactly five feet ten inches."

    "How much deeper are you going?" said the professor.

    "I am going twice as deep," was the answer, "and then my head will be twice as far below ground as it is now above ground."

    Rackbrane now asks if you could tell how deep that hole would be when finished.

    Sources:

  • THE TRUSSES OF HAY

    Farmer Tompkins had five trusses of hay, which he told his man Hodge to weigh before delivering them to a customer. The stupid fellow weighed them two at a time in all possible ways, and informed his master that the weights in pounds were `110, 112, 113, 114, 115, 116, 117, 118, 120`, and `121`. Now, how was Farmer Tompkins to find out from these figures how much every one of the five trusses weighed singly? The reader may at first think that he ought to be told "which pair is which pair," or something of that sort, but it is quite unnecessary. Can you give the five correct weights? Sources:

  • MR. GUBBINS IN A FOG

    Mr. Gubbins, a diligent man of business, was much inconvenienced by a London fog. The electric light happened to be out of order and he had to manage as best he could with two candles. His clerk assured him that though both were of the same length one candle would burn for four hours and the other for five hours. After he had been working some time he put the candles out as the fog had lifted, and he then noticed that what remained of one candle was exactly four times the length of what was left of the other.

    When he got home that night Mr. Gubbins, who liked a good puzzle, said to himself, "Of course it is possible to work out just how long those two candles were burning to-day. I'll have a shot at it." But he soon found himself in a worse fog than the atmospheric one. Could you have assisted him in his dilemma? How long were the candles burning?

    Sources:

  • THE MUDDLETOWN ELECTION

    At the last Parliamentary election at Muddletown `5,473` votes were polled. The Liberal was elected by a majority of `18` over the Conservative, by `146` over the Independent, and by `575` over the Socialist. Can you give a simple rule for figuring out how many votes were polled for each candidate? Sources:

  • THE SUFFRAGISTS' MEETING

    At a recent secret meeting of Suffragists a serious difference of opinion arose. This led to a split, and a certain number left the meeting. "I had half a mind to go myself," said the chair-woman, "and if I had done so, two-thirds of us would have retired." "True," said another member; "but if I had persuaded my friends Mrs. Wild and Christine Armstrong to remain we should only have lost half our number." Can you tell how many were present at the meeting at the start? Sources:

  • THE LEAP-YEAR LADIES

    Last leap-year ladies lost no time in exercising the privilege of making proposals of marriage. If the figures that reached me from an occult source are correct, the following represents the state of affairs in this country.

    A number of women proposed once each, of whom one-eighth were widows. In consequence, a number of men were to be married of whom one-eleventh were widowers. Of the proposals made to widowers, one-fifth were declined. All the widows were accepted. Thirty-five forty-fourths of the widows married bachelors. One thousand two hundred and twenty-one spinsters were declined by bachelors. The number of spinsters accepted by bachelors was seven times the number of widows accepted by bachelors. Those are all the particulars that I was able to obtain. Now, how many women proposed?

    Sources: