Algebra, Equations
An equation is a statement that two mathematical expressions are equal. Solving an equation involves finding the values of variables that make the statement true. Questions cover various types: linear, quadratic, polynomial, rational, radical, and systems of equations.
Diophantine Equations-
Question
There are three sacks of nuts. The first sack has `6` kilograms of nuts less than the other two sacks combined. The second sack has `10` kilograms of nuts less than the other two sacks combined.
How many kilograms of nuts are in the third sack?
Sources: -
The Restless Fly
Cities A and B are 300 kilometers apart. Two cyclists start simultaneously from A and B, heading towards each other. Their speeds are constant and equal to `30` km/h and `20` km/h, respectively. At the same moment, a fly departs from city A, flying at a speed of `100` km/h. The fly overtakes the first cyclist and flies until it meets the cyclist who left from city B. The moment the fly meets the cyclist, it immediately turns around and flies back until it meets the first cyclist again, and then it turns around again, and so on, until the cyclists meet. How many kilometers did the fly travel?
Topics:Arithmetic Algebra -> Equations Logic -> Reasoning / Logic Algebra -> Word Problems -> Motion Problems -
Question
Nina and Meir left their home at the same time and went to visit their grandmother. The route from their home to their grandmother's house is 3 km long, and benches are located along it.
Nina sits on every bench along the way to eat one cookie. She eats each cookie for the same whole number of minutes. Meir also stops and sits on every bench to eat one cookie.
It takes Meir twice as long as Nina to eat a cookie. It is also known that Nina walks at a speed of 3 km/h, and Meir at a speed of 4 km/h.
It turned out that Meir and Nina arrived at their grandmother's house at the same time.
How many benches were along the way? Find all the possibilities and justify your answer.
Sources:- Gillis Mathematical Olympiad, 2015-2016 Question 1
-
Question
Given a natural number `A`. When it is increased by `1`, its square increases by `1001`. Find `A`.
-
Question
The distinct real numbers `x` and `y` satisfy the equation:
`x^2 – 2000x = y^2 – 2000y`
Find the sum of `x` and `y`.
-
Question
Solve the equation:
`(x + 2010)(x + 2011)(x + 2012) = (x + 2011)(x + 2012)(x + 2013) `
Sources: -
Question
Given a cone (with an axis of symmetry in its center, perpendicular to its base) with a height of 6 and a base that is a circle with radius `sqrt2`. A cube is inscribed within the cone – it rests on the cone's base and all its upper vertices touch the cone. Find the side length of the cube. Justify your answer.
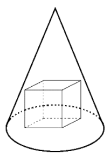 Sources:Topics:Geometry -> Solid Geometry / Geometry in Space Algebra -> Equations Geometry -> Plane Geometry -> Pythagorean Theorem Geometry -> Plane Geometry -> Triangles -> Triangle Similarity
Sources:Topics:Geometry -> Solid Geometry / Geometry in Space Algebra -> Equations Geometry -> Plane Geometry -> Pythagorean Theorem Geometry -> Plane Geometry -> Triangles -> Triangle Similarity- Gillis Mathematical Olympiad, 2015-2016 Question 2
-
Coins and Cakes
Miriam has coins of two shekels and of five shekels.
If she pays only with two-shekel coins, she will be 60 shekels short of buying 4 cakes.
If she pays only with five-shekel coins, she will be 60 shekels short of buying 5 cakes.
In total, she is 60 shekels short of buying 6 cakes. How much does a cake cost?
Sources:- Beno Arbel Olympiad, 2013, Grade 7 Question 2
-
Question
It is known that `a+b-c=6`, `ac+bc-ab=2`. Find `a^2+b^2+c^2`.
-
Question
Given real numbers `a`, `b` and `c` distinct from `0` that satisfy: `a+b/c=b+c/a=c+a/b=1`. Prove that `ab+bc+ca=0`.