קומבינטוריקה, תורת הגרפים

תורת הגרפים חוקרת גרפים, שהם מבנים המורכבים מקדקודים (צמתים) וקשתות המחברות ביניהם. היא משמשת למדידת יחסים. שאלות מכסות נושאים כמו מסלולים, מעגלים, קשירות, צביעת גרפים, עצים וניתוח תכונות של סוגי גרפים שונים.

  • העלמה הדועכת

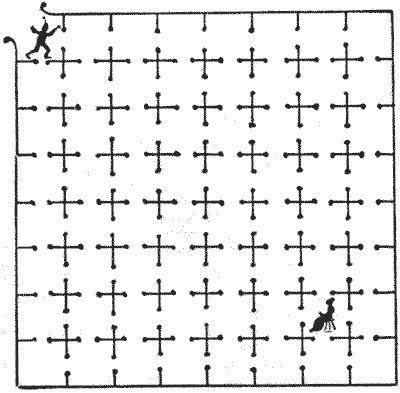    ברון מרושע בימים הטובים של פעם כלא עלמה חפה מפשע באחד הצינוקים העמוקים ביותר מתחת לחפיר הטירה. ניתן לראות מהאיור שלנו שהיו שישים ושלושה תאים בצינוק, כולם מחוברים בדלתות פתוחות, והעלמה הייתה כבולה בתא שבו היא מוצגת. כעת, אביר אמיץ, שאהב את העלמה, הצליח להציל אותה מהאויב. לאחר שהשיג כניסה לצינוק בנקודה שבה הוא נראה, הוא הצליח להגיע לעלמה לאחר שנכנס לכל תא פעם אחת בלבד. קחו את העיפרון שלכם ונסו להתחקות אחר מסלול כזה. לאחר שהצלחתם, נסו לגלות מסלול בעשרים ושניים נתיבים ישרים דרך התאים. ניתן לעשות זאת במספר הזה מבלי להיכנס לאף תא פעם שנייה. מקורות:

  • חידת מבוך

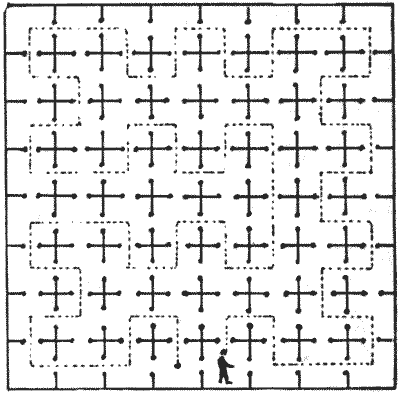    אסיר צרפתי, בשל חטאיו (או חטאיהם של אחרים), נכלא במבוך תת-קרקעי המכיל שישים וארבעה תאים, שכולם מתקשרים עם פתחי דלתות פתוחים, כפי שמוצג באיור שלנו. כדי להפחית את השעמום של חייו המוגבלים, הוא הציב לעצמו חידות שונות, וזו אחת מהן. החל מהתא שבו הוא מוצג, כיצד הוא יכול לבקר בכל תא פעם אחת, ורק פעם אחת, ולבצע כמה שיותר פניות? הניסיון הראשון שלו מוצג על ידי המסלול המקווקו. יתברר שיש לא פחות מחמישים וחמישה קווים ישרים בנתיב שלו, אבל אחרי ניסיונות רבים הוא השתפר בכך. האם אתה יכול להשיג יותר מחמישים וחמישה? אתה רשאי לסיים את הנתיב שלך בכל תא שתרצה. נסה את החידה עם עיפרון על דיאגרמות של לוח שחמט, או שאתה יכול להתייחס אליהם כאל מסעי צריחים על לוח. מקורות:

  • האריה והאיש

    במקום ציבורי ברומא עמד פעם בית כלא המחולק לשישים וארבעה תאים, כולם פתוחים לשמים וכולם מתקשרים זה עם זה, כפי שמוצג באיור. הספורט שהתקיים כאן נצפה ממגדל גבוה. המשחק האהוב היה להציב נוצרי בתא פינתי אחד ואריה בתא הפינתי הנגדי באלכסון, ואז להשאיר אותם עם כל הדלתות הפנימיות פתוחות. התוצאה הנובעת מכך הייתה לעיתים קרובות מצחיקה ביותר. באחד המקרים קיבל האיש חרב. הוא לא היה פחדן, והיה להוט למצוא את האריה בדיוק כפי שהאריה ללא ספק היה להוט למצוא אותו.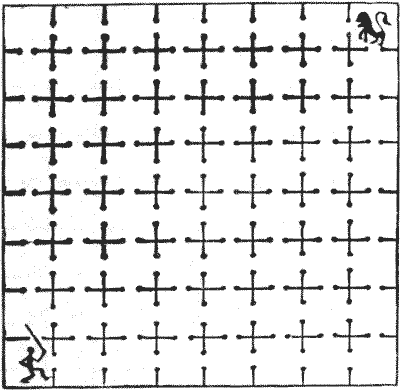 האיש ביקר בכל תא פעם אחת בלבד במספר הקטן ביותר האפשרי של קווים ישרים עד שהגיע לתא של האריה. האריה, באופן מוזר, גם הוא ביקר בכל תא פעם אחת בלבד במספר הקטן ביותר האפשרי של קווים ישרים עד שהגיע לבסוף לתא של האיש. הם התחילו יחד והלכו באותה מהירות; עם זאת, למרות שהם מדי פעם ראו זה את זה, הם מעולם לא נפגשו. החידה היא להראות את המסלול שכל אחד מהם עשה. מקורות:

  • ביקור אפיסקופלי

    המשבצות הלבנות על לוח השחמט מייצגות את הקהילות של דיוקסיה. הניחו את הרץ על כל משבצת שתרצו, ותכננו כך ש (תוך שימוש בתנועת הרץ הרגילה בשחמט) הוא יבקר בכל אחת מהקהילות שלו במספר המהלכים המועט ביותר האפשרי. כמובן, כל הקהילות שעוברים דרכן בכל מהלך נחשבות כ"ביקורות". אתם יכולים לבקר בכל משבצת יותר מפעם אחת, אך אסור לכם לנוע פעמיים בין אותן שתי משבצות סמוכות. מהו מספר המהלכים המועט ביותר האפשרי? הרץ לא צריך לסיים את ביקורו בקהילה ממנה יצא לדרך לראשונה. מקורות:

  • חידת מונה חדשה

    הנה חידה חדשה עם הזזת מונים, או מטבעות, שמבט ראשון נראית כאילו היא פשוטה באופן אבסורדי. אבל יתברר שהיא מעט מבלבלת. אני מציג אותה כאן מסיבה שאסביר כשאגיע לחידה הבאה. העתק את הדיאגרמה הפשוטה, מוגדלת, על דף נייר; ואז הנח שני מונים לבנים על הנקודות `1` ו-`2`, ושני מונים אדומים על `9` ו-`10`. החידה היא לגרום לאדומים ולבנים להחליף מקומות. אתה רשאי להזיז את המונים אחד בכל פעם בכל סדר שתרצה, לאורך הקווים מנקודה לנקודה, עם ההגבלה היחידה שמונה אדום ולבן לעולם לא יעמדו בבת אחת על אותו קו ישר. לכן המהלך הראשון יכול להיות רק מ-`1` או `2` ל-`3`, או מ-`9` או `10` ל-`7`.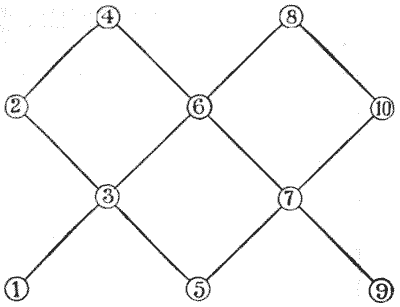 מקורות:

  • החידה החדשה של הרץ

     

    זוהי חידה קטנה ומסקרנת למדי. הניחו שמונה רצים (ארבעה שחורים וארבעה לבנים) על לוח השחמט המצומצם, כפי שמוצג באיור. הבעיה היא לגרום לרצים השחורים להחליף מקומות עם הלבנים, כך שאף רץ לא יתקוף רץ אחר מצבע מנוגד. הם חייבים לנוע לחלופין—תחילה רץ לבן, אחר כך רץ שחור, אחר כך רץ לבן, וכן הלאה. כאשר תצליחו לעשות זאת בכלל, נסו למצוא את מספר המהלכים המינימלי האפשרי.

    אם תוציאו את הרצים שעומדים על משבצות שחורות, ותשחקו רק על המשבצות הלבנות, תגלו שהחידה האחרונה שלי הסתובבה על צידה.

    מקורות:

  • פאזל הכוכבים

     

    הניחו את חוד העיפרון שלכם על אחד הכוכבים הלבנים ו(מבלי להרים את העיפרון מהדף) מחקו את כל הכוכבים בארבעה עשר קווים ישרים רציפים, כשאתם מסיימים בכוכב הלבן השני. הקווים הישרים שלכם יכולים להיות בכל כיוון שתרצו, רק כל פנייה חייבת להתבצע על כוכב. אין התנגדות למחוק כוכב כלשהו יותר מפעם אחת.

    במקרה הזה, כאשר ריבועי ההתחלה והסיום שלכם מקובעים בצורה לא נוחה, אינכם יכולים להשיג פתרון על ידי שבירת מסע מלכה, או בכל דרך אחרת באמצעות מסעי מלכה בלבד. אבל מותר לכם להשתמש בקווים ישרים אלכסוניים —כגון מהכוכב הלבן העליון ישירות לכוכב פינתי.

    מקורות:

  • המחליקן המדעי

     

    ניתן לראות שהמחליקן סימן על הקרח שישים וארבע נקודות או כוכבים, והוא מציע להתחיל מהמיקום הנוכחי שלו ליד הפינה ולהיכנס לכל אחת מהנקודות בארבעה עשר קווים ישרים. איך הוא יעשה זאת? כמובן שאין התנגדות לכך שהוא יעבור על פני כל נקודה יותר מפעם אחת, אבל המהלך הישר האחרון שלו חייב להחזיר אותו למיקום שממנו הוא התחיל.

    זה רק עניין של לקחת את העיפרון ולהתחיל מהמקום שבו רגלו של המחליקן נחה כרגע, ולמחוק את כל הכוכבים בארבעה עשר קווים ישרים רצופים, ולחזור לנקודה ממנה יצאתם.

    מקורות:

  • ארבעים ותשעה הכוכבים

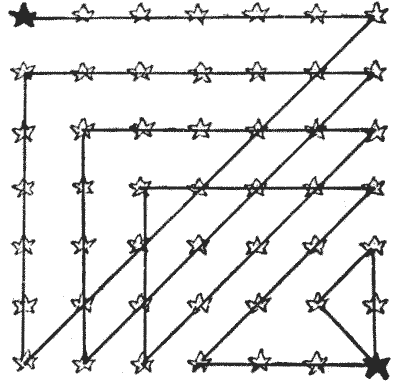    החידה במקרה זה היא פשוט לקחת את העיפרון שלך, ולהתחיל מכוכב שחור אחד, למחוק את כל הכוכבים בשנים עשר קווים ישרים, ולסיים בכוכב השחור השני. ניתן לראות שהניסיון המוצג באיור דורש חמישה עשר קווים. האם אתה יכול לעשות זאת בשנים עשר? כל פנייה חייבת להתבצע על כוכב, והקווים חייבים להיות מקבילים לצדדים ולאלכסונים של הריבוע, כפי שמוצג. במקרה זה אנו עוסקים בלוח שחמט בעל ממדים מופחתים, אך נדרשים רק מהלכי מלכה (מבלי לצאת מגבולות הלוח, כפי שהיה במקרה האחרון). מקורות:

  • סנט ג'ורג' והדרקון

    הנה חידה קטנה על לוח שחמט מצומצם של ארבעים ותשעה משבצות. סנט ג'ורג' רוצה להרוג את הדרקון. הריגת דרקונים הייתה בילוי ידוע שלו, וכאביר, זה היה טבעי שהוא ירצה לבצע את המשימה בסדרת מהלכי פרש. האם תוכלו להראות כיצד, החל מהמשבצת המרכזית, הוא יכול לבקר פעם אחת בלבד בכל משבצת בלוח בשרשרת של מהלכי פרש, ולסיים בלכידת הדרקון במהלך האחרון שלו? כמובן שמגוון דרכים שונות פתוחות בפניו, אז נסו לגלות מסלול שיוצר עיצוב נאה כלשהו כאשר סימנתם כל קפיצה עוקבת על ידי קו ישר ממשבצת למשבצת. מקורות: